Matrice d'une application linéaire. Bijective ?
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
- MatricesMatrices
- DéterminantsDéterminants de matrices
Énoncé du sujet
Soit 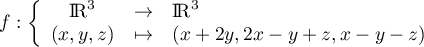
- Monter que
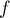 est linéaire et donner sa matrice
dans la base canonique de
est linéaire et donner sa matrice
dans la base canonique de  .
.
-
 est-elle bijective ?
est-elle bijective ?
Correction
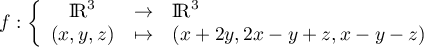
Correction
Soit-
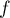 est clairement linéaire et sa matrice
dans la base canonique de
est clairement linéaire et sa matrice
dans la base canonique de 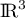 est:
est:
![\[\lb\begin{array}{rrr}1&2&0 \\ 2&-1&1 \\ 1&-1&-1\enar\rb\]](/Generateur-Devoirs/Colles/determinants/exApplication-lineaire-bijective_c/4.png)
- On calcule le déterminant de la matrice de
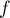 ,
en développant, par exemple, suivant la 1ère ligne,
,
en développant, par exemple, suivant la 1ère ligne,
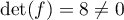 , et donc
, et donc 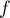 est bijective.
est bijective.
Tags:Applications linéairesMatricesDéterminants
Autres sujets au hasard:

Voir aussi: