Lien suite et série

Colle de mathématiques

Sujet de colle de maths:

On considère une suite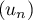

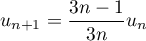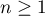donnée par $u_1\geq0$ et $u_{n+1}=\dfrac{3n-1}{3n} u_n$ pour $n\geq 1$ .

Démontrer que 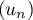converge.
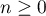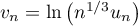On pose, pour $n\geq 0$ , $v_n=\ln\left( n^{1/3}u_n\rp$ .
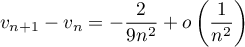Démontrer que $v_{n+1}-v_n=-\dfrac2{9n^2}+o\lp\dfrac 1{n^2}\rp$ .
En déduire que la série de terme général 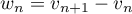$w_n=v_{n+1}-v_n$ converge.
En déduire que la suite 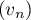converge. On notera 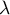$\lambda$ sa limite.
Donner un équivalent simple de . La série de terme général 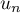est-elle convergente?

Correction

On a directement que

$\begin{array}{ll}\dfrac{u_{n+1}}{u_n}&=\dfrac{3n-1}{3n}\\ &=1-\dfrac1{3n}\leq1\enar$

et donc, comme la suite est positive (par une récurrence immédiate), on en déduit que la suite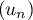 est décroissante, et minorée, donc convergente.
On a

$\begin{array}{lcl} v_{n+1}-v_n&=\ln\lp(n+1)^{1/3}u_{n+1}\rp-\ln\lp n^{1/3}u_n\rp\\[.8em] &=\ln\lp\dfrac{(n+1)^{1/3}u_{n+1}}{n^{1/3}u_n}\rp\\[1.2em] &=\ln\lp\lp\dfrac{n+1}{n}\rp^{1/3}\tm\dfrac{u_{n+1}}{u_n}\rp\\[1.2em] &=\ln\lp\lp1+\dfrac1n\rp^{1/3}\dfrac{3n-1}{3n}\rp\\[1.4em] &=\dfrac13\ln\lp1+\dfrac1n\rp+\ln\lp1-\dfrac1{3n}\rp \enar$

puis, en utilisant le développement limité du logarithme,

$\begin{array}{ll} v_{n+1}-v_n&=\dfrac13\lp\dfrac1n-\dfrac{1}{2n^2}\right) -\dfrac1{3n}-\dfrac1{2(3n)^2} +o\lp\dfrac1{n^2}\rp\\[1.2em] &=-\dfrac2{9n^2}+o\lp\dfrac1{n^2}\right) \enar$
On a

$w_n=v_{n+1}-v_n\sim\dfrac{-2}{9n^2}$

et donc, par comparaison avec une série de Riemann convergente, la série de terme général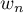 est convergente.
On passe maintenant d'une série télescopique à une suite:

$\sum_{n=1}^{N-1}w_n=\sum_{n=1}^{N-1}(v_{n+1}-v_n)=v_N-v_0$

et, puisque la série est convergente, il en est de même de la suite .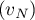
On a

$\lim_{n\to+\infty}\ln(n^{1/3}u_n=\lambda$

et donc,

$u_n\sim\dfrac{e^{\lambda}}{n^{1/3}}$

et ainsi, par comparaison avec une série de Riemann divergente, la série de terme général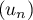 est aussi divergente.

Tag:Séries

Autres sujets au hasard:

Voir aussi: