Intégrale impropre: convergence, calcul avec changement de variable


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

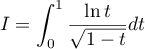Justifier la convergence et calculer la valeur de l'intégrale: $I=\dsp\int_0^{1}\dfrac{\ln t}{\sqrt{1-t}}dt$.
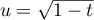On pourra utiliser le changement de variable $u=\sqrt{1-t}$.


Correction

Correction

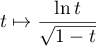La fonction $t\mapsto\dfrac{\ln t}{\sqrt{1-t}}$ est continue sur $]0;1[$. Il faut étudier la convergence en 0 et 1.

En 0, on a
\[f(t)=\dfrac{\ln t}{\sqrt{1-t}}\sim\ln(t)\]

qui est intégrable en 0.

En 1, on a (éventuellement en posant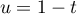 $u=1-t$)
\[f(t)=\dfrac{\ln t}{\sqrt{1-t}}\sim\dfrac{t-1}{\sqrt{1-t}} =-\sqrt{1-t}\]

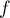et $f$ est donc prolongeable par continuité en 0 par 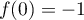$f(0)=-1$, et en particulier 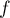$f$ est intégrable en 0.

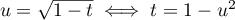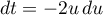Avec le changement de variable $u=\sqrt{1-t}\iff t=1-u^2$, et $dt=-2u\,du$, on obtient:
\[\begin{array}{lcl} I=\dsp\int_0^1 \frac{\ln t}{\sqrt{1-t}}dt &=&2\dsp\int_0^1 \ln(1-u^2)du\\[1em] &=&\dsp\int_0^1 \ln\Bigl(1-u)(1+u)\Bigr)du\\[1em] &=&\dsp2\int_0^1 \ln(1-u)du+2\int_0^1 \ln(1+u)du\\ \enar\]

puis avec les changements de variable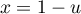 $x=1-u$ dans la première intégrale et 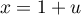$x=1+u$ dans la deuxième (ou en utiisant directement une primitive 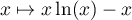$x\mapsto x\ln(x)-x$ du logarithme), on obtient
\[\begin{array}{lcl} I&=&2\dsp\int_0^1 \ln(x)dx+2\int_1^2\ln(x)dx\\[1em] &=&2\dsp\int_0^2 \ln(x)dx\\[.8em] &=&2\Bigl[x\ln x-x\Bigr]_0^2\\[.8em] &=&4\ln 2-4 \enar\]



Tag:Intégrale

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0