Homothétie d'une loi exponentielle
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit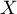 
une variable aléatoire de loi exponentielle de paramètre 
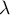et soit 
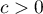un réel.
Déterminer la loi de la variable aléatoire 
.
une variable aléatoire de loi exponentielle de paramètre
et soit un réel.
Déterminer la loi de la variable aléatoire .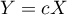
Correction
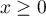, on a
![\[P(cX\leq x) =P\left( X\leq \dfrac{x}c\right)
=1-\exp\lp-\dfrac{\lambda x}c\rp\]](/Generateur-Devoirs/Colles/VAC/c-loi-exp_c/2.png)
où on reconnaît la fonction de répartition d'une variable aléatoire exponentielle de paramètre
.
Correction
Pour tout réel, on a
où on reconnaît la fonction de répartition d'une variable aléatoire exponentielle de paramètre
.
Tag:Variables aléatoires continues
Autres sujets au hasard:
