Gain aux fléchettes
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
On lance une fléchette sur une cible circulaire de rayon égal à 1 mètre.
La probabilité d'atteindre une zone donnée de la cible est proportionnelle
à l'aire de cette zone.
- On note R la distance séparant le centre de la cible de la fléchette. Déterminer la loi de R.
- Pour participer au jeu, on mise 1 euro, et on gagne à chaque fois
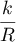 euros.
euros.
On note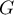 le gain algébrique du joueur.
Calculer l'espérance de
le gain algébrique du joueur.
Calculer l'espérance de 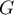 .
.
- L'organisateur espère gagner 0,20 euro par partie en moyenne.
Quelle valeur doit-il donner à k ?
Dans la suite, k prend cette valeur. - Quels sont les gains possibles du joueur ? Que vaut
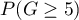 ?
Et
?
Et  ?
?
Correction
Correction
- On a
![$R(\Omega)=[0;1]$](/Generateur-Devoirs/Colles/VAC/flechettes-aleatoires_c/1.png) , et pour
, et pour ![$r\in[0;1]$](/Generateur-Devoirs/Colles/VAC/flechettes-aleatoires_c/2.png) ,
on a
,
on a 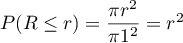 .
.
La densité de probabilité s'obtient alors par dérivation: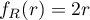 si
si 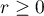 ,
, 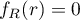 sinon.
sinon.
- Le gain est
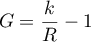 , et son espérance
, et son espérance
![\[\begin{array}{ll}E(G)&=\dsp\int_0^1\lp\dfrac{k}r-1\rp2rdr\\[1em]
&=2k\dsp\int_0^1dr-2\int_0^1rdr\\[.8em]
&=2k-1\enar\]](/Generateur-Devoirs/Colles/VAC/flechettes-aleatoires_c/8.png)
- L'organisateur veut donc
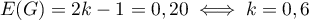 .
.
- Comme
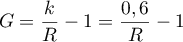 ,
on a
,
on a 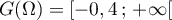 ,
et
,
et
![\[P(G\geq5)=P\lp\dfrac{0,6}R-1\geq5\right)
=P\left( R\leq0,1\rp=0,1^2=0,01\]](/Generateur-Devoirs/Colles/VAC/flechettes-aleatoires_c/12.png)
donc 1% de chance de gagner plus de 5 euros, et
![\[P(G\geq0)=P\lp\dfrac{0,6}R-1\geq0\right)
=P\left( R\leq0,6\rp=0,6^2=0,36\]](/Generateur-Devoirs/Colles/VAC/flechettes-aleatoires_c/13.png)
donc environ 1 chance sur trois d'être gagnant, donc aussi environ deux chances sur trois d'être perdant.
Tag:Variables aléatoires continues
Autres sujets au hasard:
