Exponentielle itérées
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit 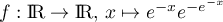 .
.
- Montrer que f est une densité de probabilité.
- Soit
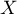 une variable admettant
une variable admettant 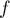 pour densité.
Déterminer la loi de
pour densité.
Déterminer la loi de 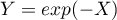 et son espérance.
et son espérance.
- Établir que
 possède une espérance.
possède une espérance.
Correction
Correction
-
 est clairement positive et continue et de plus
est clairement positive et continue et de plus
![\[\int_{-\infty}^{+\infty}e^{-x}e^{-e^{-x}}dx
=\left[ e^{-e^{-x}}\rb_{-\infty}^{+\infty}=1-0=1\]](/Generateur-Devoirs/Colles/VAC/expexp_c/2.png)
ce qui finit de montrer que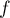 est bien une densité de probabilité.
est bien une densité de probabilité.
- On a
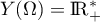 et, pour
et, pour 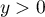 ,
,
![\[F_Y(y)=P(Y\leq y)=P(X\geq-\ln(y))=1-F_X(-\ln(y))
=e^{-y}\]](/Generateur-Devoirs/Colles/VAC/expexp_c/6.png)
d'où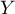 suit la loi exponentielle
suit la loi exponentielle 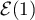 .
.
On a alors directement aussi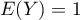 .
.
-
![\[E(X)=E(-\ln(Y))
=\int_0^{+\infty}-ln(y)e^{-y}dy\]](/Generateur-Devoirs/Colles/VAC/expexp_c/10.png)
Il s'agit d'une intégrale généralisée, d'une fonction continue sur![$]0;+\infty[$](/Generateur-Devoirs/Colles/VAC/expexp_c/11.png) .
.
Il reste donc à vérifier que cette intégrale converge aussi en 0 et .
.
En 0, on a
![\[-\ln(y)e^{-y}\sim -\ln(y)\]](/Generateur-Devoirs/Colles/VAC/expexp_c/13.png)
qui est intégrable en 0 (ce qu'on peut redémontrer en utilisant une primitive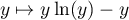 de
de 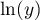 ).
).
En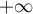 , on a par croissances comparées
, on a par croissances comparées
![\[\lim_{y\to+\infty}y^2\lp-\ln(y)e^{-y}\rp=0\]](/Generateur-Devoirs/Colles/VAC/expexp_c/17.png)
c'est-à-dire que
![\[-\ln(y)e^{-y}\underset{+\infty}{=}o\lp\dfrac1{y^2}\rp\]](/Generateur-Devoirs/Colles/VAC/expexp_c/18.png)
et est donc convergente par comparaison avec une intégrale de Riemann (avec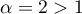 ).
).
Ainsi l'intégrale existe et l'espérance aussi.
Tag:Variables aléatoires continues
Autres sujets au hasard:
