Suite récurrente avec une densité de probabilité

Colle de mathématiques

Sujet de colle de maths:

Variables aléatoires continuesVariables aléatoires continues

Énoncé du sujet

Oral ESCP, BL - 2021
Soit

l'application définie sur $\R$ par:

$\forall t\in\R,\, f(t)=\dfrac{2e^t}{\sqrt{1+t^2}}$

Faire une étude rapide de la fonction : domaine de définition, variations, limites aux bornes du domaine de définition, asymptotes éventuelles.
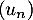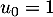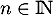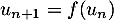On considère la suite réelle définie par et pour tout $n\in\N$ , $u_{n+1} = f (u_n)$ .
On admet que, pour tout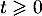 $t\geqslant0$ , on a : .
Étudier la limite éventuelle de la suite .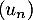
On considère l'application 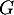définie sur 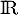$\R$ par

$\forall x\in\R,\, G(x)=\int_{-x}^xf(t)dt$

Étudier les variations de .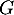
Étudier la limite éventuelle de la suite .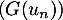

Correction

Oral ESCP, BL - 2021

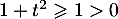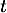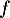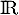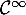Comme $1+t^2\geqslant1>0$ pour tout réel , la fonction est définie et dérivable sur $\R$ , et même de classe $\mathcal{C}^\infty$ .
On calcule

$\begin{array}{ll}f'(t)&=2\dfrac{e^t\sqrt{1+t^2}-e^t\dfrac{2t}{2\sqrt{1+t^2}}}{1+t^2}\\ &=2e^t\dfrac{t^2-t+1}{(1+t^2)^{3/2}} \enar$

Le trinôme du numérateur a un discriminant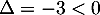 $\Delta=-3<0$ donc n'admet pas de racine et il est ainsi toutjours strictement positif.
On en déduit que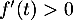 et donc 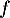strictement croissante sur $\R$ .
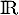Par croissances comparées, on trouve les limites

$\lim_{t\to-\infty}f(t)=0$

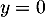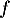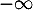et la droite d'équation (l'axe des abscisses) est donc asymptote à la courbe de en $-\infty$ , tandis que

$\lim_{t\to+\infty}f(t)=+\infty$
Comme 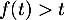, on a donc 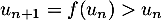$u_{n+1}=f(u_n)>u_n$ et la suite est donc croissante.
On a donc l'aternative: soit la suite est majorée et elle aussi convergente, soit elle diverge vers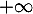 $+\infty$ .
Or, si elle converge, c'est vers un point fixe de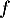 , c'est-à-dire vers une limite 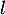telle que 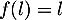. Or, on admet ici que c'est impossible pour 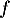pour laquelle .
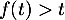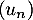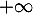On en déduit que, nécessairement, diverge vers $+\infty$ .
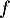est continue sur 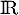$\R$ et admet donc une primitive 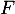sur $\R$ .
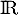On a alors

$G(x)=F(x)-F(-x)$

et donc

$\begin{array}{ll}G'(x)&=F'(x)+F'(-x)\\ &=f(x)+f(-x)\\ &=2\dfrac{e^x+e^{-x}}{\sqrt{1+x^2}}>0 \enar$

d'où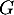 est strictement croissante sur $\R$ .

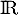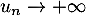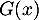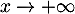On se rappelle que $u_n\to+\infty$ , et on cherche donc la limite de lorsque $x\to+\infty$ .
On a vu aussi que pour la fonction à intégrer,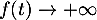 $f(t)\to+\infty$ lorsque 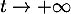$t\to+\infty$ et ainsi

$\int_0^{+\infty}f(t)dt$

diverge grossièrement.
Par contre

$\int_{-\infty}^0f(t)dt$

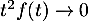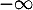converge puisque $t^2f(t)\to0$ en $-\infty$ , par croissances comparées.
Finalement la somme

$\int_{-\infty}^0f(t)dt+\int_0^{+\infty}f(t)dt$

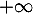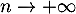diverge vers $+\infty$ , comme lorsque $n\to+\infty$ .

Tag:Variables aléatoires continues

Autres sujets au hasard:

Voir aussi: