Étude de la convergence de la série

Colle de mathématiques

Sujet de colle de maths:

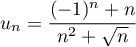
Étudier la convergence de la série de terme général $u_n=\dfrac{(-1)^n+n}{n^2+\sqrt{n}}$

Correction

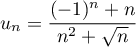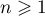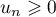La série de terme général $u_n=\dfrac{(-1)^n+n}{n^2+\sqrt{n}}$ n'est pas alternée, car pour $n\geqslant1$ , $u_n\geqslant0$ .
On a de plus

$u_n=\dfrac{(-1)^n+n}{n^2+\sqrt{n}}\sim\dfrac{n}{n^2}=\dfrac1n$

qui est le terme général d'une série de Riemann divergente, et la série est aussi donc divergente.

Tag:Séries

Autres sujets au hasard:

Voir aussi: