Étude de la convergence de la série
Étudier la convergence de la série de terme général
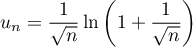
Correction
On a, en 0,
, et donc ici,
![\[u_n=\dfrac1{\sqrt{n}}\ln\lp1+\dfrac1{\sqrt{n}}\right)
\sim \dfrac1{\sqrt{n}}\tm\dfrac1{\sqrt{n}}
=\dfrac1n\]](/Generateur-Devoirs/Colles/Series/excvg4_c/2.png)
qui est le terme général d'une série de Riemann divergente, et la série est aussi donc divergente.
Cacher la correction
On a, en 0,
, et donc ici,
qui est le terme général d'une série de Riemann divergente, et la série est aussi donc divergente.
Cacher la correction
Tag:Séries
Autres sujets au hasard:
