Étude de la convergence de la série
Colle de mathématiques
Sujet de colle de maths:- SériesSéries
Énoncé du sujet
Étudier la convergence de la série de terme général
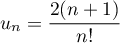
Correction
![\[\begin{array}{ll}\dfrac{u_{n+1}}{u_n}&=\dfrac{2(n+2)}{(n+1)!}\tm\dfrac{n!}{2(n+1)} \\[.8em]
&=\dfrac{n+2}{(n+1)^2}\underset{+\infty}{\sim}\dfrac1n\to0\enar\]](/Generateur-Devoirs/Colles/Series/excvg5_c/1.png)
ce qui montre, d'après la règle de d'Alembert, que la série est convergente.
Correction
On ace qui montre, d'après la règle de d'Alembert, que la série est convergente.
Tag:Séries
Autres sujets au hasard:
Voir aussi: