Étude de fonction, bijection et réciproque
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
Énoncé du sujet
- Rappeler la définition d'une fonction bijective.
- Démontrer que la fonction
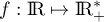 définie par
définie par 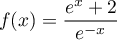 est bijective.
est bijective.
- Tracer l'allure de la courbe
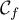 de
de 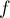 , après avoir préciser les limites de
, après avoir préciser les limites de  en l'infini, et l'équation de la tangente en 0.
en l'infini, et l'équation de la tangente en 0.
- Donner l'expression de sa fonction réciproque
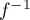 et tracer sur le graphique précédent l'allure de sa courbe.
et tracer sur le graphique précédent l'allure de sa courbe.
Correction
Correction
- voir cours...
-
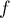 est dérivable sur
est dérivable sur 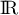 avec
avec
![\[\begin{array}{ll}f'(x)&=\dfrac{e^xe^{-x}-(e^x+2)(-e^{-x})}{(e^{-x})^2}\\[1em]
&=2\dfrac{1+e^{-x}}{e^{-2x}}\enar\]](/Generateur-Devoirs/Colles/Calcul/exFR2_c/3.png)
et, comme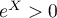 pour tout réel
pour tout réel 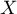 , on a aussi
, on a aussi 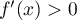 ,
et donc
,
et donc 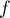 est strictement croissante sur sur
est strictement croissante sur sur 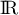 .
.
Comme de plus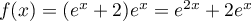 , on a
, on a
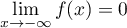 et
et
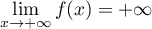 on en déduit que
on en déduit que 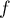 est une bijection de
est une bijection de 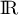 sur
sur 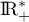 .
.
- On a
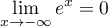 et
et 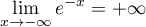 ,
d'où
,
d'où 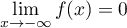 .
.
On en déduit en particulier que l'axe des abscisses (droite d'équation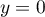 ) est une asymptote en
) est une asymptote en 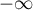 à
à 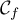 .
.
En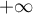 , on a
, on a 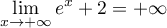 et
et
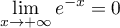 avec
avec 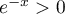 d'où, par quotient des limites,
d'où, par quotient des limites,
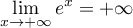 .
.
La tangente en 0 a pour équation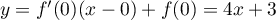 .
.
Voir à la fin pour la courbe. - Pour déterminer sa fonction réciproque, on pose
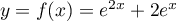 , pour
, pour 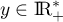 et on cherche à exprimer
et on cherche à exprimer 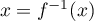 .
.
Soit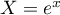 , alors on a
, alors on a  .
C'est une équation du second degré de déterminant
.
C'est une équation du second degré de déterminant  car
car 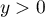 , et qui admet donc deux solutions réelles
, et qui admet donc deux solutions réelles
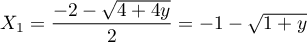 et
et
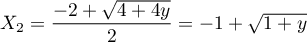 .
.
Comme on a posé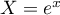 et que
et que 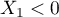 on a une seule solution:
on a une seule solution:
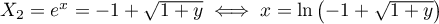 .
.
Ainsi, la fonction réciproque de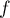 est définie par
est définie par
![\[f^{-1}\la\begin{array}{lcl}R_+^*&\to&\R\\ y&\mapsto&\ln\lp-1+\sqrt{1+y}\rp\enar\right.\]](/Generateur-Devoirs/Colles/Calcul/exFR2_c/40.png)
Pour tracer sa courbe, on se rappelle que les courbe de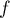 et de
et de 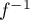 sont symétriques par rapport à la 1ère bissectrice (droite
sont symétriques par rapport à la 1ère bissectrice (droite  )
)
{3}
\psplot[linewidth=1.2pt,linecolor=blue]{-5}{5}{2.718 x exp 2 add 2.718 x -1 mul exp div}
\rput(.5,10){\blue$\mathcal{C}_f$}
\psplot{-5}{4}{4 x mul 3 add}
\psplot[linewidth=1.2pt,linecolor=red]{.01}{5}{-1 1 x add .5 exp add ln}
\rput(5,1){\red$\mathcal{C}_{f^{-1}}$}
\rput(3,.4){3}
\psplot{-5}{5}{x}\rput(4,4.7){$y=x$}
\end{pspicture*}\]](/Generateur-Devoirs/Colles/Calcul/exFR2_c/44.png)
Tag:Dérivée
Autres sujets au hasard:

Voir aussi: