Dérivée d'une somme géométrique
Colle de mathématiques
Sujet de colle de maths:- SuitesSuites
- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
- SommesSommes des termes d'une suite
Énoncé du sujet
Pour 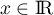 et
et  , calculer la somme
, calculer la somme
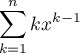 .
.
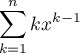 .
.
Correction
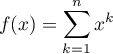 .
.
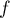 est dérivable sur
est dérivable sur 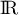 (et même
(et même 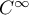 ),
et on a, pour tout réel
),
et on a, pour tout réel 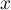 ,
,
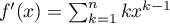 .
.
Par ailleurs, on a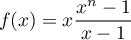 , et donc
, et donc
![\[\begin{array}{ll}
f'(x)&=\dfrac{x^n-1}{x-1}+x\dfrac{nx^{n-1}(x-1)-\left( x^n-1\right)}{(x-1)^2}\\[1em]
&=\dfrac{\left( x^n-1\rp(x-1)+nx^n(x-1)-x\left( x^n-1\rp}{(x-1)^2} \\[1em]
&=\dfrac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2} \\
\enar\]](/Generateur-Devoirs/Colles/Suites/ex11_c/8.png)
On a ainsi,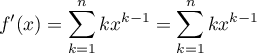 .
.
Correction
Soit la fonction polynôme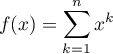 .
.
Par ailleurs, on a
![\[\begin{array}{ll}
f'(x)&=\dfrac{x^n-1}{x-1}+x\dfrac{nx^{n-1}(x-1)-\left( x^n-1\right)}{(x-1)^2}\\[1em]
&=\dfrac{\left( x^n-1\rp(x-1)+nx^n(x-1)-x\left( x^n-1\rp}{(x-1)^2} \\[1em]
&=\dfrac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2} \\
\enar\]](/Generateur-Devoirs/Colles/Suites/ex11_c/8.png)
On a ainsi,
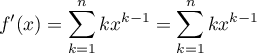 .
.
Tags:SuitesDérivéeSommes
Autres sujets au hasard:

Voir aussi: