Étude de fonction, bijection et réciproque
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
Énoncé du sujet
Soit  la fonction définie par l'expression
la fonction définie par l'expression
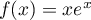 .
.
- Étudier les variations de
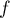 .
.
Préciser la tangente à la courbe de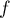 à l'origine.
à l'origine.
- Justifier que
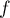 réalise une bijection de
réalise une bijection de 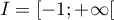 sur un intervalle
sur un intervalle 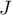 que l'on précisera.
que l'on précisera.
- Tracer dans un repère l'allure de
 et celle de sa fonction réciproque.
et celle de sa fonction réciproque.
- On note
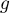 la fonction réciproque de
la fonction réciproque de 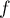 .
Montrer que, pour
.
Montrer que, pour 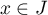 et
et 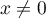 ,
,
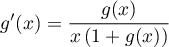 .
.
Correction
Correction
-
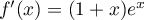 , ainsi
, ainsi 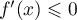 et
et 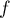 est décroissante
sur
est décroissante
sur ![$]-\infty;-1]$](/Generateur-Devoirs/Colles/Calcul/exFR_c/4.png) , et
, et 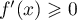 et
et 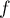 croissante sur
croissante sur
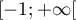 .
.
On peut compléter avec les limites: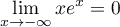 , par croissances comparées,
et
, par croissances comparées,
et
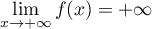 .
.
À l'origine, en , la tangente a pour équation
, la tangente a pour équation
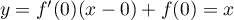 .
.
-
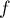 est donc une bijection entre
est donc une bijection entre 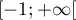 et
et 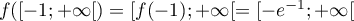 .
.
- Les courbes de
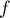 et de sa réciproque sont symétriques
par rapport à la droite d'équation
et de sa réciproque sont symétriques
par rapport à la droite d'équation  .
.
- Comme
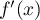 ne s'annule pas sur
ne s'annule pas sur ![$]-1;+\infty[$](/Generateur-Devoirs/Colles/Calcul/exFR_c/18.png) ,
,
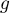 est dérivable sur
est dérivable sur ![$]-e^{-1};+\infty[$](/Generateur-Devoirs/Colles/Calcul/exFR_c/20.png) .
.
Comme f(g(x))=x pour tout![$x\in]-e^{-1};+\infty[$](/Generateur-Devoirs/Colles/Calcul/exFR_c/21.png) ,
on obtient en dérivant,
,
on obtient en dérivant,
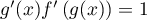 ,
soit
,
soit 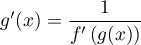 .
.
Or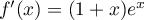 , donc
, donc
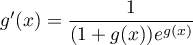 ,
,
et de plus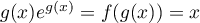 ,
donc aussi
,
donc aussi 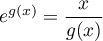 .
.
Ainsi,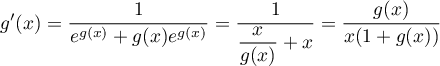 .
.
Tag:Dérivée
Autres sujets au hasard:
