Étude d'une fonction

Colle de mathématiques

Sujet de colle de maths:

DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)

Énoncé du sujet

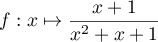Étudier le sens de variation de la fonction $f:x\mapsto \dfrac{x+1}{x^2+x+1}$ .
Tracer l'allure de sa courbe représentative.

Correction

Le trinôme

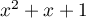pour discriminant 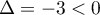$\Delta=-3<0$ et donc ne s'annule jamais sur 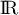$\R$ , et ainsi

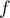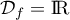est définie sur $\mathcal{D}_f=\R$ .
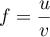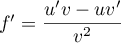On a de plus $f=\dfrac{u}{v}$ et $f'=\dfrac{u'v-uv'}{v^2}$ ,
soit, pour tout

réel,

$\begin{array}{ll}f'(x)&=\dfrac{1\left( x^2+x+1\rp-(x+1)(2x+1)}{\left( x^2+x+1\rp^2} \\[.8em] &=\dfrac{-x^2-2x}{\left( x^2+x+1\rp^2} =\dfrac{-x(x+2)}{\left( x^2+x+1\rp^2}\enar$

On obtient alors le tableau de variation:

$\begin{tabular}{|c|ccccccc|}\hline $x$ & $-\infty$ && $-2$ && $0$ && $+\infty$ \\\hline $-x^2-x$ && $-$ &\zb& $+$ &\zb&$-$& \\\hline $x^2+x+1$ && $+$ & $|$ &$+$&$|$ & $+$ &\\\hline $f'(x)$ && $-$ &\zb& $+$ &\zb&$-$& \\\hline &0&&&&1&&\\ $f$&&{\Large$\searrow$}&&{\Large$\nearrow$}&&{\Large$\searrow$}&\\ &&&$-\frac13$&&&&0\\\hline \end{tabular}$

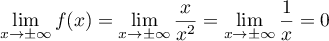
en ajoutant les limites: $\dsp\lim_{x\to\pm\infty}f(x)=\lim_{x\to\pm\infty}\dfrac{x}{x^2} =\lim_{x\to\pm\infty}\dfrac{1}{x}=0$
On a donc l'allure:

$\begin{pspicture}(-5,-1)(5,2) \psline[arrowsize=7pt]{->}(-5,0)(5,0) \psline[arrowsize=7pt]{->}(0,-1)(0,2) \psline(-2,.1)(-2,-.1)\rput(-2,.2){$-2$} \psline(1,.1)(1,-.1)\rput(1,-.3){$1$} \psline(-.1,1)(.1,1)\rput(-.2,1.25){$1$} \psplot[linewidth=1.5pt,linecolor=blue]{-5}{5}{x 1 add x 2 exp x add 1 add div} \end{pspicture}$

Tag:Dérivée

Autres sujets au hasard:

Voir aussi: