Espérance et fonction de répartition
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit  une densité de probabilité d'une variable aléatoire
une densité de probabilité d'une variable aléatoire 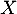 à valeurs dans
à valeurs dans 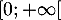 , et
, et 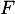 sa fonction de répartition.
On note:
sa fonction de répartition.
On note:
![\[\forall t\geqslant0,\ Q(t) =1-F(t)\]](/Generateur-Devoirs/Colles/VAC/Efp/5.png)
On suppose qu'il existe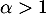 tel que
tel que
![\[\lim_{t\to+\infty}t^\alpha Q(t)=0\]](/Generateur-Devoirs/Colles/VAC/Efp/7.png)
On suppose qu'il existe
- Montrer que
![$E[X]$](/Generateur-Devoirs/Colles/VAC/Efp/8.png) existe et que
existe et que
![\[E[X]=\int_0^{+\infty}Q(t)\,dt\]](/Generateur-Devoirs/Colles/VAC/Efp/9.png)
- Soit
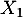 , … ,
, … , 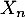 ,
, 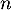 variables aléatoires indépendantes,
toutes de loi exponentielle de paramètre 1.
variables aléatoires indépendantes,
toutes de loi exponentielle de paramètre 1.
On note .
.
Déterminer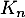 la fonction de répartition de
la fonction de répartition de 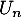 .
.
En déduire l'espérance et la variance de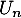 .
.
- Soit
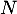 qui suit une loi géométrique de paramètre
qui suit une loi géométrique de paramètre ![$p\in]0, 1[$](/Generateur-Devoirs/Colles/VAC/Efp/18.png) .
On note
.
On note 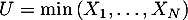 .
.
Déterminer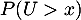 pour tout
pour tout 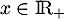 .
.
La variable aléatoire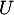 admet-elle une espérance ? Si oui, la calculer.
admet-elle une espérance ? Si oui, la calculer.
Correction
Soit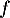 une densité de probabilité d'une variable aléatoire
une densité de probabilité d'une variable aléatoire 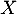 à valeurs dans
à valeurs dans 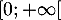 .
On note:
.
On note:
![\[\forall t\geqslant0,\ Q(t) =1-F(t)\]](/Generateur-Devoirs/Colles/VAC/Efp_c/4.png)
On suppose qu'il existe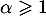 tel que
tel que
![\[\lim_{t\to+\infty}t^\alpha Q(t)=0\]](/Generateur-Devoirs/Colles/VAC/Efp_c/6.png)
Correction
Oral ENSAE - Saclay - 2019Soit
On suppose qu'il existe
-
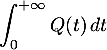 converge par comparaison avec une intégrale de Riemann car
converge par comparaison avec une intégrale de Riemann car 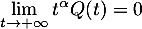 avec
avec 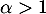 .
.
En intégrant alors par parties avec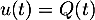 et
et 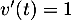 ,
on a
,
on a
![\[\int_0^{+\infty}Q(t)\,dt
=\Bigl[\,Q(t) t\,\Bigr]_0^{+\infty}-\int_0^{+\infty}Q'(t)t\,dt\]](/Generateur-Devoirs/Colles/VAC/Efp_c/12.png)
où- [
 ]
] 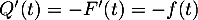 et donc
et donc
![\[-\int_0^{+\infty}Q'(t)t\,dt=\int_0^{+\infty}tf(t)\,dt=E(X)\]](/Generateur-Devoirs/Colles/VAC/Efp_c/15.png)
- [
 ]
pour tout
]
pour tout 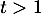 , et comme
, et comme 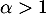 , on a le théorème des gendarmes
, on a le théorème des gendarmes
![\[0\leqslant tQ(t)\leqslant t^\alpha Q(t)\underset{t\to+\infty}{\to}0\]](/Generateur-Devoirs/Colles/VAC/Efp_c/19.png)
d'où
![\[\Bigl[\,Q(t) t\,\Bigr]_0^{+\infty}=0\]](/Generateur-Devoirs/Colles/VAC/Efp_c/20.png)
![\[E[X]=\int_0^{+\infty}Q(t)\,dt\]](/Generateur-Devoirs/Colles/VAC/Efp_c/21.png)
- [
- On a, par indépendance,
![\[\begin{array}{lcl}K_n(t)&=&P(U_n\leqslant t)\\
&=&1-P(U_n\geqslant t)\\
&=&1-P\left( X_1\geqslant t \cap \dots X_n\geqslant t\rp\\
&=&1-\dsp\prod_{i=1}^nP(X_i\geqslant t)\\
&=&1-\left( e^{-x}\rp^n=1-e^{-nx}
\enar\]](/Generateur-Devoirs/Colles/VAC/Efp_c/22.png)
La variable aléatoire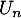 suit donc la loi exponentielle de paramètre
suit donc la loi exponentielle de paramètre 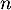 ,
et on a donc aussi, en particulier
,
et on a donc aussi, en particulier
![\[E[U_n]=\dfrac1n\]](/Generateur-Devoirs/Colles/VAC/Efp_c/25.png)
et
![\[V[X]=\dfrac1{n^2}\]](/Generateur-Devoirs/Colles/VAC/Efp_c/26.png)
- De même que précédemment, on a maintenant, pour
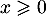 ,
,
![\[\begin{array}{lcl}P(U>x)&=&\sum_{n=1}^{+\infty}P(U>x\cap N=n)\\
&=&\dsp\sum_{n=1}^{+\infty}P(U_n>x\cap N=n)\\
&=&\dsp\sum_{n=1}^{+\infty}P(U_n>x)(N=n)\\
&=&\dsp\sum_{n=1}^{+\infty}e^{-nx}pq^{n-1}\\
&=&\dfrac{p}q\dsp\sum_{n=1}^{+\infty}\left( qe^{-x}\rp^n\\
&=&\dfrac{p}qqe^{-x}\dfrac1{1-qe^{-x}}\\
&=&\dfrac{pe^{-x}}{1-qe^{-x}}
\enar\]](/Generateur-Devoirs/Colles/VAC/Efp_c/28.png)
Maintenant, d'après la première question, avec
![\[Q(x)=\dfrac{pe^{-x}}{1-qe^{-x}}\]](/Generateur-Devoirs/Colles/VAC/Efp_c/29.png)
qui vérifie bien, par croissances comparées,
![\[\lim_{x\to+\infty}x^2Q(x)=\lim_{x\to+\infty}px^2e^{-x}=0\]](/Generateur-Devoirs/Colles/VAC/Efp_c/30.png)
On a vu alors que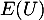 existe avec
existe avec
![\[\begin{array}{lcl}E(U)&=&\dsp\int_0^{+\infty}Q(x)dx\\[1.2em]
&=&\dsp\int_0^{+\infty}\dfrac{pe^{-x}}{1-qe^{-x}}dx\\[1.2em]
&=&\lb\,\dfrac{p}q\ln\lp1-qe^{-x}\rp\,\rb_0^{+\infty}\\[1.2em]
&=&\dfrac{p}q\ln(1-q)
\enar\]](/Generateur-Devoirs/Colles/VAC/Efp_c/32.png)
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: