Équation différentielle - 2nd ordre, coefficients constants


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

Résoudre 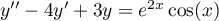$y''-4y'+3y=e^{2x}\cos(x)$


Correction

Correction

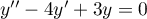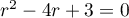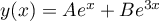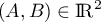L'équation homogène associée $y''-4y'+3y=0$ a pour équation caractéristique $r^2-4r+3=0$ de racines $r=1$ et $r=3$, et donc pour solutions $y(x)=Ae^x+Be^{3x}$, $(A,B)\in\R^2$.

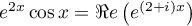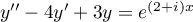Comme $e^{2x}\cos x=\Re e\left( e^{(2+i)x}\rp$, on peut chercher une rechercher une solution particulière de l'équation $y''-4y'+3y=e^{(2+i)x}$ et en prendre la partie réelle ensuite.
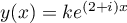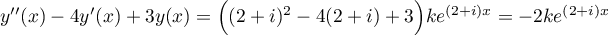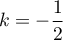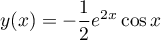On recherche une telle solution particulière sous la forme $y(x)=ke^{(2+i)x}$, pour laquelle $y''(x)-4y'(x)+3y(x)=\Bigl((2+i)^2-4(2+i)+3\Bigr)ke^{(2+i)x} =-2ke^{(2+i)x}$. Il suffit donc de choisir $k=-\dfrac12$ et la solution partiulière $y(x)=-\dfrac12e^{2x}\cos x$.


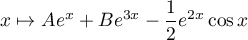Les solutions de l'équation sont donc les fonctions $x\mapsto Ae^x+Be^{3x}-\dfrac12e^{2x}\cos x$.


Tag:Équation différentielle

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0