Équation différentielle - 1er ordre, coefficients non constants
Colle de mathématiques
Sujet de colle de maths:- Équation différentielleÉquation différentielle
Énoncé du sujet
Résoudre: 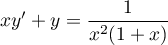
Correction
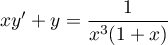
L'équation homogène est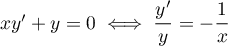 soit
soit 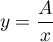 ,
, 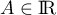 .
.
En faisant varier la constante, on trouve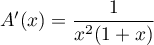 .
.
Pour intégrer ce terme, on décompose en éléments simples:
![\[\dfrac{1}{x^2(1+x)}
=\dfrac{1+x-x}{x^2(1+x)}
=\dfrac{1}{x^2}-\dfrac{1}{x(1+x)}
=\dfrac{1}{x^2}-\dfrac{1+x-x}{x(1+x)}
=\dfrac{1}{x^2}-\dfrac{1}{x}+\dfrac{1}{1+x}\]](/Generateur-Devoirs/Colles/EquaDiff/ex5.1_c/6.png)
et donc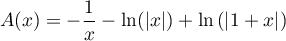 .
.
Les solutions de l'équation sont donc les fonctions ,
,
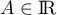 .
.
Correction
L'équation homogène est
En faisant varier la constante, on trouve
Pour intégrer ce terme, on décompose en éléments simples:
et donc
Les solutions de l'équation sont donc les fonctions
Tag:Équation différentielle
Autres sujets au hasard:
