Équation différentielle - 1er ordre, coefficients constants
Colle de mathématiques
Sujet de colle de maths:- Équation différentielleÉquation différentielle
Énoncé du sujet
Résoudre: 
Correction
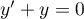 et a pour solutions
les fonctions
et a pour solutions
les fonctions 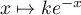 ,
,  .
.
Faisons varier la constante: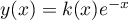 ,
alors
,
alors 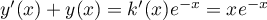 et donc
et donc 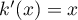 ,
d'où
,
d'où 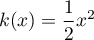 .
.
Ainsi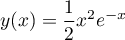 est une solution particulière,
et les solutions générales sont
est une solution particulière,
et les solutions générales sont
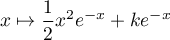 ,
,  .
.
Correction
L'équation homogène estFaisons varier la constante:
Ainsi
Tag:Équation différentielle
Autres sujets au hasard:
