Équation de la tangente à un cercle passant par un point donné
Colle de mathématiques
Sujet de colle de maths:- Géométrie plane cartésienneGéométrie plane cartésienne, géométrie et coordonnées dans le plan
Énoncé du sujet
Dans le plan muni d'un repère orthonormal 
,
déterminer les équations des tangentes au cerle
de centre 
et de rayon 5 et qui passent par
.
,
déterminer les équations des tangentes au cerle
de centre 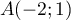et de rayon 5 et qui passent par
.
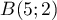Correction
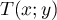un point de tangence sur le cercle,
alors on a
![\[\begin{array}{l}
\la\begin{array}{l}
\overrightarrow{AT}\cdot\overrightarrow{BT}=(x+2)(x-5)+(y-1)(y-2)=0\\[.5em]
AT^2=(x+2)^2+(y-1)^2=5^2=25
\enar\right.
\iff
\la\begin{array}{l}
x^2+y^2-3x-3y-8=0\\[.5em]
x^2+y^2+4x-2y-20=0
\enar\right.\\[1.5em]
\iff
\la\begin{array}{l}
x^2+y^2-3x-3y-8=0\\[.5em]
7x+y-12=0
\enar\right.\\[1.5em]
\iff
\la\begin{array}{l}
x^2+(-7x+12)^2-3x-3(-7x+12)-8=50x^2-150x+100=0\\[.5em]
y=-7x+12=0
\enar\right.\\[1.5em]
\end{array}
\]](/Generateur-Devoirs/Colles/Geom2D/ex5_c/2.png)
est une racine évidente du trinôme,
la 2ème racine étant alors 
.
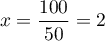On trouve donc deux possibilités: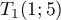
et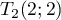 
.
Soit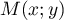
un point d'une tangente, alors
![\[\begin{array}{ll}\overrightarrow{AT_1}\cdot\overrightarrow{BM}=0&\iff3(x-5)+4(y-2)=0\\[.4em]&\iff3x+4y-23=0\enar\]](/Generateur-Devoirs/Colles/Geom2D/ex5_c/8.png)
ou
![\[\begin{array}{ll}\overrightarrow{AT_2}\cdot\overrightarrow{BM}=0&\iff4(x-5)+1(y-2)=0\\[.4em]&\iff 4x+y-22=0\enar\]](/Generateur-Devoirs/Colles/Geom2D/ex5_c/9.png)
Correction
Soit un point de tangence sur le cercle,
alors on a
est une racine évidente du trinôme,
la 2ème racine étant alors . On trouve donc deux possibilités:
et .
Soit
un point d'une tangente, alors
ou
Tag:Géométrie plane cartésienne
Autres sujets au hasard:
Voir aussi: