Minimisation d'une intégrale
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
- IntégraleIntégrale
Énoncé du sujet
Calculer
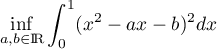 .
.
Correction
![$E=\mathcal{C}([0,1])$](/Generateur-Devoirs/Colles/EspaceEuclidien/ex5_c/1.png) muni du produit scalaire
muni du produit scalaire
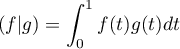 .
.
On a alors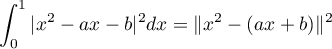 ,
et, avec
,
et, avec 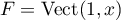 ,
,
![\[\inf_{(a,b)\in\R^2}\int_0^1 |x^2-ax-b|^2dx=\inf_{f\in F}\|x^2-f\|^2.
=\inf_{f\in F}\|x^2-f\|=\|x^2-p(x^2)\|\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex5_c/5.png)
où est la projection orthogonale de
est la projection orthogonale de 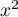 sur
sur 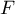 . Il s'agit donc
de calculer cette projection. Ceci peut se faire de deux façons.
D'une part, on peut fabriquer une base orthonormale de
. Il s'agit donc
de calculer cette projection. Ceci peut se faire de deux façons.
D'une part, on peut fabriquer une base orthonormale de 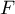 par le procédé de Gram-Schmidt
à partir de
par le procédé de Gram-Schmidt
à partir de  et on sait que
et on sait que
![\[p(x^2)=(x^2|e_1)e_1+(x^2|e_2)e_2.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex5_c/11.png)
On peut aussi poser a priori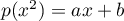 et écrire que
et écrire que  ,
, 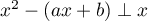 .
On obtient le système :
.
On obtient le système :
![\[\la\begin{array}{ccc}
\dsp\int_0^1 x^2-(ax+b)dx&=&0\\[.8em]
\dsp\int_0^1 x^3-(ax^2+bx)dx&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex5_c/15.png)
qui permet de calculer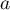 et
et  .
Par l'une ou l'autre méthode, on trouve que
.
Par l'une ou l'autre méthode, on trouve que 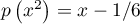 et donc
que
et donc
que 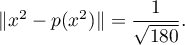
Correction
SoitOn a alors
où
On peut aussi poser a priori
![\[\la\begin{array}{ccc}
\dsp\int_0^1 x^2-(ax+b)dx&=&0\\[.8em]
\dsp\int_0^1 x^3-(ax^2+bx)dx&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex5_c/15.png)
qui permet de calculer
Tags:Espaces euclidiensIntégrale
Autres sujets au hasard:

Voir aussi: