Diagonalisation d'une matrice 4x4
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
- MatricesMatrices
Énoncé du sujet
Soit 

-
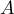 est-elle diagonalisable ?
est-elle diagonalisable ?
- Déterminer les éléments propres de
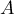 .
.
Correction
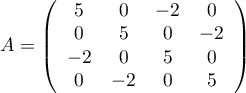
Correction
Soit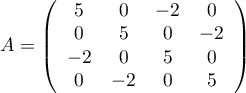
- Le polynôme caractéristique de
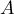 est
est
![\[\begin{array}{lcl}\chi_A(X)&=&\det\left( XI-A\rp\\[.9em]
&=&\left|\begin{array}{cccc}x-5&0&2&0\\0&x-5&0&2\\2&0&x-5&0\\0&2&0&x-5\enar\right|\\[3em]
&=&(x-5)\left|\begin{array}{ccc}x-5&0&2\\0&x-5&0\\2&0&x-5\enar\right|\\
&&+2\left|\begin{array}{ccc}0&2&0\\x-5&0&2\\2&0&x-5\enar\right|\\[2em]
&=&(x-5)\Bigl( (x-5)\left|\begin{array}{cc}x-5&0\\0&x-5\enar\right|\\
&&\phantom{(x-5)\ }+2\left|\begin{array}{cc}0&2\\x-5&0\enar\right|\Bigr)\\[2em]
&&+2\left( -2\left|\begin{array}{ccc}x-5&2\\2&x-5\enar\right|\ \rp\\[1.6em]
&=&(x-5)\Bigl((x-5)^3-4(x-5)\Bigr)-4\Bigl((x-5)^2-4\Bigr)\\
&=&(x-5)^2\Bigl((x-5)^2-4\Bigr)-4\Bigl((x-5)^2-4\Bigr)\\
&=&\Bigl((x-5)^2-4\Bigr)\Bigl((x-5)^2-4\Bigr)\\
&=&\Bigl((x-5)^2-4\Bigr)^2\\
&=&\Bigl(\lp(x-5)-2\rp\lp(x-5+2\rp\Bigr)^2\\
&=&(x-7)^2(x-3)^2
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex3_c/3.png)
Le polynôme caractéristique est scindé, avec deux valeurs propres: et
et  .
.
Pour savoir si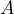 est diagonalisable, il reste encore à déterminer la dimension des espaces propres
associés.
est diagonalisable, il reste encore à déterminer la dimension des espaces propres
associés.
- Espace propre associé à
 .
.
Soit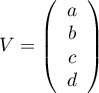 alors
alors
![\[\begin{array}{ll}AV=3V&\iff
\la\begin{array}{cccc}
2a-2c=0\\2b-2d=0\\-2a+2c=0\\-2b+2d=0
\enar\right.\\[2.5em]
&\iff
\bigl( a=c \text{ et } b=d\bigr)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex3_c/9.png)
Ainsi, l'espace propre est de dimension 2 avec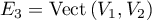 avec
avec
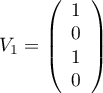 et
et
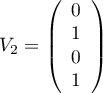 .
.
Espace propre associé à .
.
Soit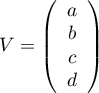 alors
alors
![\[\begin{array}{ll}AV=7V&\iff
\la\begin{array}{cccc}
-2a-2c=0\\-2b-2d=0\\-2a-2c=0\\-2b-2d=0
\enar\right.\\[2.5em]
&\iff
\bigl( a=-c \text{ et } b=-d\bigr)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex3_c/15.png)
Ainsi, l'espace propre est aussi de dimension 2 avec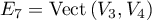 avec
avec
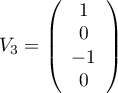 et
et
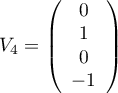 .
.
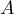 est donc diagonalisable dans la base
est donc diagonalisable dans la base
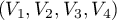 .
.
Tags:DiagonalisationMatrices
Autres sujets au hasard:

Voir aussi: