Diagonalisabilité et base de polynômes propres
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
Énoncé du sujet
Oral ESCP, BL - 2021
Soit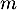 un entier naturel non nul. On considère l'espace vectoriel
un entier naturel non nul. On considère l'espace vectoriel ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6/2.png) des fonctions polynomiales de degré inférieur ou égal à
des fonctions polynomiales de degré inférieur ou égal à 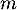 et l''application
et l''application  associant à tout polynôme
associant à tout polynôme 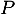 de
de ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6/6.png) , le polynôme
, le polynôme 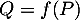 défini par
défini par
![\[Q(x)=m(x-1)P(x)-x(x-1)P'(x)\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6/8.png)
pour tout réel , et où
, et où 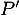 désigne le polynôme dérivé de
désigne le polynôme dérivé de 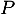 .
.
Soit
pour tout réel
- Montrer que
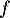 est un endomorphisme de
est un endomorphisme de ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6/13.png) .
.
- Montrer que si
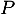 est un vecteur propre de
est un vecteur propre de 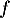 , alors 0 ou 1 sont racines de
, alors 0 ou 1 sont racines de  .
.
- Pour tout entier naturel
 , on note
, on note 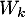 la fonction polynomiale de
la fonction polynomiale de ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6/19.png) définie par:
définie par:
![\[W_k(x)=x^k(x-1)^{m-k}\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6/20.png)
Montrer que pour tout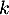 ,
, 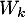 est un vecteur propre de
est un vecteur propre de 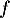 .
.
- Quelles sont les valeurs propres de l'endomorphisme
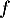 ?
L'endomorphisme
?
L'endomorphisme  est-il diagonalisable ?
est-il diagonalisable ?
- Montrer que
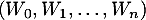 est une base de
est une base de ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6/27.png) et déterminer les composantes du polynôme constant
et déterminer les composantes du polynôme constant 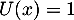 dans cette base.
dans cette base.
Correction
Correction
Oral ESCP, BL - 2021- La linéarité de
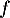 provient directement de celle de la dérivé:
soit deux polynômes
provient directement de celle de la dérivé:
soit deux polynômes  et
et 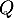 , un réel
, un réel 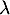 et
et 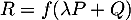 , alors
, alors
![\[\begin{array}{lcl}R(x)&=&m(x-1)(\lambda P+Q)(x)-x(x-1)(\lambda P+Q)'(x)\\
&=&m(x-1)(\lambda P+Q)(x)-x(x-1)(\lambda P'+Q')(x)\\
&=&\lambda m(x-1)P(x)-x(x-1)P'(x)\\
&&+m(x-1)Q(x)-x(x-1)Q'(x)\\
&=&\lambda f(P)(x)+f(Q)(x)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/6.png)
ce qui montre que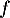 est linéaire.
est linéaire.
Il reste à montrer que, pour![$P\in\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/8.png) on a aussi
on a aussi ![$f(P)\in\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/9.png) , c'est-à-dire que
, c'est-à-dire que 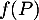 est un polynôme de degré inférieur ou égal à
est un polynôme de degré inférieur ou égal à 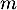 .
.
On peut le faire avec un polynôme quelconque de![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/12.png) ou, maintenant qu'on a montré la linéarité, se contenter de le faire pour une base de
ou, maintenant qu'on a montré la linéarité, se contenter de le faire pour une base de ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/13.png) , par exemple les polynômes
, par exemple les polynômes 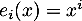 , pour
, pour 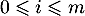 .
.
On a
![\[f(e_i)(x)=m(x-1)x^i-ix(x-1)x^{i-1}\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/16.png)
qui est un polynôme de degré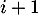 si
si 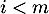 , donc
, donc ![$f(e_i)\in\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/19.png) .
.
Par contre, si , on trouve ici que
, on trouve ici que 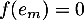 et donc aussi que
et donc aussi que
![$f(e_m)\in\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/22.png) .
.
Par linéarité, on a donc que![$f(P)\in\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/23.png) pour tout
pour tout ![$P\in\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/24.png) et donc
et donc 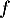 est un endomorphisme de
est un endomorphisme de ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/26.png) .
.
- Soit
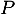 un vecteur propre de
un vecteur propre de 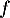 , c'est-à-dire
, c'est-à-dire 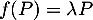 ,
soit
,
soit
![\[m(x-1)P(x)-x(x-1)P'(x)=\lambda P(x)\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/30.png)
Maintenant, pour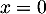 on a
on a
![\[-mP(0)=\lambda P(0)\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/32.png)
et pour on a
on a
![\[0=\lambda P(1)\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/34.png)
Si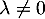 alors on a donc
alors on a donc  , sinon, si
, sinon, si 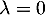 , on a
, on a  .
.
Finalement, quelque soit la valeur propre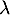 , 0 ou 1 est une racine de
, 0 ou 1 est une racine de 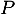 .
.
- Il suffit de calculer
 . On a
. On a
![\[W_k'(x)=kx^{k-1}(x-1)^{m-k}+(m-k)x^k(x-1)^{m-k-1}\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/42.png)
et on trouve, toiut calculs faits,
![\[f(W_k)=(k-m)W_k\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/43.png)
et qui montre que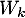 est vecteur propre associé à la valeur propre
est vecteur propre associé à la valeur propre 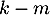 .
.
- Pour
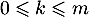 ,
,  est valeur propre de
est valeur propre de 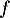 , qui admet donc
, qui admet donc 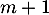 valeurs propres distincts dans l'espace
valeurs propres distincts dans l'espace ![$\R_m[x]$](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/50.png) qui est de dimension
qui est de dimension  .
.
On en déduit que est donc diagonalisable.
est donc diagonalisable.
- Pour tout
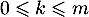 ,
, 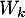 est un vecteur propre de
est un vecteur propre de  associé à la valeur propre
associé à la valeur propre 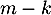 .
La famille
.
La famille 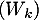 forme donc une base vecteurs propres de
forme donc une base vecteurs propres de  .
.
Pour décomposer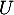 , on cherche donc les coefficients
, on cherche donc les coefficients 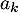 tels que
tels que
![\[\begin{array}{ll}U(x)=1&=\dsp\sum_{k=0}^ma_kW_k(x)\\
&=\dsp\sum_{k=0}^ma_kx^k(x-1)^{m-k}\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/61.png)
En choisissant pour les coefficients binômomiaux, on a justement la formule du binôme de Newton:
les coefficients binômomiaux, on a justement la formule du binôme de Newton:
![\[\sum_{k=0}^m\binom{m}{k}x^k(-1)^{m-k}(x-1)^{m-k}=\biggl(x-(x-1)\biggr)^m=1\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.6_c/63.png)
Tag:Diagonalisation
Autres sujets au hasard:
