Deux équations du second degré
Colle de mathématiques
Sujet de colle de maths:- ComplexesNombres complexs
Énoncé du sujet
Résoudre dans 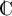 les équations
les équations
 et
et
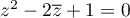
Correction
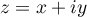 , avec
, avec 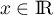 et
et 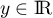 , alors
, alors
![\[\begin{array}{ll}
z^2-2\overline{z}-1=0
&\iff \Bigl(x^2-y^2-2x-1\Bigr) +i\Bigl(2xy-2y\Bigr)=0 \\[1em]
&\iff\la\begin{array}{l}x^2-y^2-2x-1=0 \\ 2xy-2y=0 \enar\right.
\enar\]](/Generateur-Devoirs/Colles/Complexes/exEq1_c/4.png)
La 2ème équation se réécrit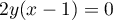 et nous donne donc
l'alternative
et nous donne donc
l'alternative 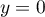 ou
ou  .
.
Si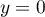 , la 1ère équation devient
, la 1ère équation devient 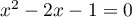 qui est du 2nd degré de discriminant
qui est du 2nd degré de discriminant 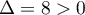 et donc de racines
et donc de racines 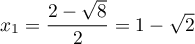 et
et 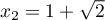 .
.
Si , la 1ère équation devient
, la 1ère équation devient 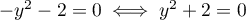 qui n'a pas de solution dans
qui n'a pas de solution dans 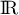 .
.
Il y a donc deux solutions, qui sont réelles: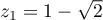 et
et 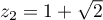 .
.
De même, pour la 2ème équation, avec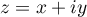 ,
,
![\[\begin{array}{ll}
z^2-2\overline{z}+1=0
&\iff \Bigl(x^2-y^2-2x+1\Bigr) +i\Bigl(2xy-2y\Bigr)=0 \\[1em]
&\iff\la\begin{array}{l}x^2-y^2-2x+1=0 \\ 2xy-2y=0 \enar\right.
\enar\]](/Generateur-Devoirs/Colles/Complexes/exEq1_c/19.png)
La 2ème équation toujours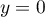 ou
ou  .
.
Si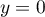 , la 1ère équation se réécrit
, la 1ère équation se réécrit 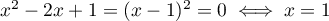
Si , la 1ère équation se réécrit
, la 1ère équation se réécrit
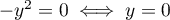 .
.
Il y ainsi aussi une seule solution: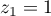 .
.
Correction
On pose![\[\begin{array}{ll}
z^2-2\overline{z}-1=0
&\iff \Bigl(x^2-y^2-2x-1\Bigr) +i\Bigl(2xy-2y\Bigr)=0 \\[1em]
&\iff\la\begin{array}{l}x^2-y^2-2x-1=0 \\ 2xy-2y=0 \enar\right.
\enar\]](/Generateur-Devoirs/Colles/Complexes/exEq1_c/4.png)
La 2ème équation se réécrit
Si
Si
Il y a donc deux solutions, qui sont réelles:
De même, pour la 2ème équation, avec
![\[\begin{array}{ll}
z^2-2\overline{z}+1=0
&\iff \Bigl(x^2-y^2-2x+1\Bigr) +i\Bigl(2xy-2y\Bigr)=0 \\[1em]
&\iff\la\begin{array}{l}x^2-y^2-2x+1=0 \\ 2xy-2y=0 \enar\right.
\enar\]](/Generateur-Devoirs/Colles/Complexes/exEq1_c/19.png)
La 2ème équation toujours
Si
Si
Il y ainsi aussi une seule solution:
Tag:Complexes
Autres sujets au hasard:

Voir aussi: