Détermination d'une limite

Colle de mathématiques

Sujet de colle de maths:

LimiteLimites de suites et de fonctions

Énoncé du sujet

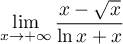
Déterminer la limite $\dsp\lim_{x\to+\infty}\dfrac{x-\sqrt{x}}{\ln x+x}$

Correction

On a

$\dfrac{x-\sqrt{x}}{\ln x+x} =\dfrac{x\lp1-\dfrac{\sqrt{x}}{x}\right)}{x\lp\dfrac{\ln x}{x}+1\right)} =\dfrac{1-\dfrac1{\sqrt{x}}}{\dfrac{\ln x}{x}+1}$

et donc, comme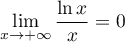 $\dsp\lim_{x\to+\infty}\dfrac{\ln x}{x}=0$ , par croissances comparées,

$\lim_{x\to+\infty}\dfrac{x-\sqrt{x}}{\ln x+x}=1$

Tag:Limite

Autres sujets au hasard:

Voir aussi: