Courbe paramétrée fractions rationnelles
Colle de mathématiques
Sujet de colle de maths:- Courbes paramétréesCourbes paramétrées
Énoncé du sujet
Étudier et tracer la courbe d'équations paramétriques:
![\[\la\begin{array}{ll}
x(t)= t+\dfrac 1t\\
y(t)=t+\dfrac 1{2t^2}
\enar\right.\]](/Generateur-Devoirs/Colles/courbesparam/ex5/1.png)
pour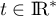
.
On étudiera en particulier la position par rapport aux asymptotes,
et la tangente aux points stationnaires.
pour
.
On étudiera en particulier la position par rapport aux asymptotes,
et la tangente aux points stationnaires.
Correction
![\[\la\begin{array}{ll}
x'(t)=1-\dfrac1{t^2}=\dfrac{(t-1)(t+1)}{t^2}\\[.8em]
y'(t)=1-\dfrac1{t^3}=\dfrac{(t-1)(t^2+t+1)}{t^3}
\enar\right.\]](/Generateur-Devoirs/Colles/courbesparam/ex5_c/1.png)
On en déduit le tableau de variations suivant :
![\[\begin{tabular}{|c|ccccccccc|}\hline
$t$ & $-\infty$ && $-1$ && 0 && 1 && $+\infty$\\\hline
$x'(t)$ && $+$ &0& $-$ &\psline(0,-3.9)(0,.3)\,\psline(0,-3.9)(0,.3)& $-$ &0&$+$&\\\hline
&&&$-2$&&&&&&\\
x&&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&2&&\\\hline
&&&&&&&&&\\
y&&\Large{$\nearrow$}&$\frac12$&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&$\frac32$&&\\\hline
$y'(t)$ && $+$ &2& $+$ &&$-$&0&$+$& \\\hline
\end{tabular}\]](/Generateur-Devoirs/Colles/courbesparam/ex5_c/2.png)
On obtient des branches infinies pour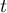
tendant vers 
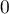et 
.
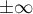Commençons par étudier la branche infinie au voisinage de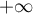 
. On a
![\[\frac{y(t)}{x(t)}=\frac{t+\frac {1}{2t^2}}{t+\frac 1{t}}\to 1.\]](/Generateur-Devoirs/Colles/courbesparam/ex5_c/7.png)
Ensuite, on a
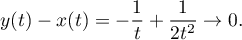
Ainsi, la droite d'équation
est asymptote à la courbe paramétrée,
et de plus, puisque 
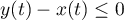pour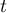 
grand:
la courbe est située au-dessous de son asymptote.
De même, pour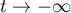
, la droite d'équation 
est aussi asymptote à la courbe.
Mais cette fois, la courbe sera située au-dessus de l'asymptote.
Étudions maintenant la branche infinie pour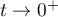
.
On a:
![\[\begin{array}{ll}\dfrac{y(t)}{x(t)}&=\dfrac{t+\frac {1}{2t^2}}{t+\frac 1{t}}\\[1em]
&=\dfrac{\frac 1{t^2}\tm(2+t^3)}{\frac 1t\times(1+t^2)}\\[1em]
&=\dfrac1t\tm\dfrac{2+t^3}{1+t^2}\to +\infty\enar\]](/Generateur-Devoirs/Colles/courbesparam/ex5_c/15.png)
La courbe admet donc une branche parabolique d'axe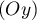
.
C'est la même chose pour 
.
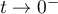Le tableau nous montre également que la courbe admet une tangente verticale au point
.
Enfin, le point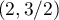
est un point singulier.
Pour déterminer la tangente à la courbe en ce point, on peut étudier
la limite en 
de
![\[\frac{y(t)-y(1)}{x(t)-x(1)}=\frac{1}{2t}\times\frac{2t^3-3t^2+1}{t^2-2t+1}.\]](/Generateur-Devoirs/Colles/courbesparam/ex5_c/21.png)
C'est une forme indéterminée, mais on peut factoriser les deux polynômes sachant que
est racine de chacun. En réalité, 1 est même racine
double, et on peut factoriser l'expression en
![\[\frac{y(t)-y(1)}{x(t)-x(1)}=\frac{1}{2t}\times (2t+1)\to \frac32\textrm{ quand }t\to 1.\]](/Generateur-Devoirs/Colles/courbesparam/ex5_c/23.png)
Ainsi, au point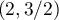
, la tangente a pour coefficient directeur 
.
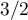On on peut aussi effectuer ce calcul en utilisant les développements limités: si on note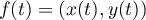
, alors 
dirige la tangente
en 
et 
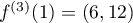ne lui est pas colinéaire,
et donc qu'on a affaire à un point de rebroussement de première espèce.
On obtient finalement la courbe suivante :
![\[\psset{unit=0.6cm,arrowsize=7pt}
\begin{pspicture*}(-12,-12)(12,12)
\psaxes{->}(0,0)(-12,-12)(12,12)
\rput(0.05,-0.1){$0$}
\parametricplot[plotpoints=200,linecolor=red,linewidth=1.5pt]{0.001}{10}{
t 1 t div add
t 1 2 t 2 exp mul div add
}
\parametricplot[plotpoints=200,linecolor=red,linewidth=1.5pt]{-10}{0.001}{
t 1 t div add
t 1 2 t 2 exp mul div add
}
\end{pspicture*}\]](/Generateur-Devoirs/Colles/courbesparam/ex5_c/30.png)
Correction
On aOn en déduit le tableau de variations suivant :
On obtient des branches infinies pour
tendant vers et .
Commençons par étudier la branche infinie au voisinage de . On a
Ensuite, on a
Ainsi, la droite d'équation
est asymptote à la courbe paramétrée,
et de plus, puisque pour grand:
la courbe est située au-dessous de son asymptote.
De même, pour
, la droite d'équation
est aussi asymptote à la courbe.
Mais cette fois, la courbe sera située au-dessus de l'asymptote.Étudions maintenant la branche infinie pour
.
On a:
La courbe admet donc une branche parabolique d'axe
.
C'est la même chose pour .
Le tableau nous montre également que la courbe admet une tangente verticale au point
.
Enfin, le point
est un point singulier.
Pour déterminer la tangente à la courbe en ce point, on peut étudier
la limite en de
C'est une forme indéterminée, mais on peut factoriser les deux polynômes sachant que
est racine de chacun. En réalité, 1 est même racine
double, et on peut factoriser l'expression en
Ainsi, au point
, la tangente a pour coefficient directeur .On on peut aussi effectuer ce calcul en utilisant les développements limités: si on note
, alors dirige la tangente
en et ne lui est pas colinéaire,
et donc qu'on a affaire à un point de rebroussement de première espèce.
On obtient finalement la courbe suivante :
Tag:Courbes paramétrées
Autres sujets au hasard:
Voir aussi: