Couple de variables géométriques
Colle de mathématiques
Sujet de colle de maths:- Couples de variables aléatoiresCouples de variables aléatoires
Énoncé du sujet
Soient 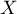 et
et 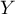 deux variables aléatoires à valeurs dans
deux variables aléatoires à valeurs dans  , telles que :
, telles que :
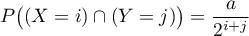 ,
pour tous
,
pour tous 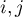 de
de  .
.
- Calculer
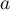 .
.
- Déterminer les lois marginales de
 et
et 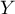 .
.
-
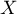 et
et 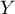 sont-elles indépendantes?
sont-elles indépendantes?
Correction
Correction
- Il faut que
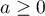 et que ensuite:
et que ensuite:
![\[\sum_{i,j\geq 1}\dfrac{a}{2^{i+j}}=1
\iff \sum_{i=1}^{+\infty}\frac{a}{2^i}=1
\iff a=1\]](/Generateur-Devoirs/Colles/CVA/Couple-geometrique_c/2.png)
- Pour
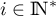 , on a :
, on a :
![\[\begin{array}{ll}
P(X=i)&=\dsp\sum_{j=1}^{+\infty}P\big((X=i)\cap(Y=j)\big)\\[1.5em]
&=\dsp\sum_{j=1}^{+\infty}\frac{1}{2^{i+j}}\\[1.5em]
&=\dfrac{1}{2^i}=\dfrac{1}{2}\dfrac{1}{2^{i-1}}\enar\]](/Generateur-Devoirs/Colles/CVA/Couple-geometrique_c/4.png)
 suit donc une loi géométrique de paramètre
suit donc une loi géométrique de paramètre 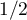 .
.
Par symétrie, il en est de même pour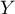 .
.
-
![\[P(X=i)\times P(Y=j)=\dfrac{1}{2^{i+j}}=P\big((X=i)\cap(Y=j)\big)\]](/Generateur-Devoirs/Colles/CVA/Couple-geometrique_c/8.png)
ce qui montre que les variables aléatoires sont indépendantes.
Tag:Couples de variables aléatoires
Autres sujets au hasard:

Voir aussi: