Caractérisation d'un endomorphisme diagonalisable
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
Énoncé du sujet
Pour des endomorphismes 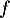 et
et 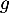 de
de 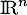 , on note
, on note 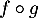 la composée de
la composée de  et
et 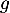 et
et 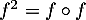 .
On note
.
On note  l’endomorphisme identité de
l’endomorphisme identité de  .
Pour un endomorphisme
.
Pour un endomorphisme 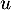 de
de  , soit
, soit 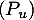 la propriété:
la propriété:
![\[\forall \lambda\in\R, Ker(u-\lambda Id) = Ker (u-\lambda Id)^2\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago/13.png)
Première partie. Soit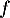 et
et 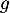 deux endomorphismes de
deux endomorphismes de 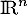 tels que
tels que 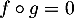 .
.
Première partie. Soit
- Montrer que
 .
.
- Montrer que
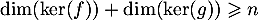 .
.
- Soit
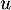 un endomorphisme de
un endomorphisme de 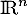 tel que
tel que
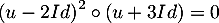 .
.
Montrer que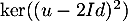 et
et  sont supplémentaires dans
sont supplémentaires dans 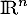 .
.
- Si
 vérifie de plus
vérifie de plus 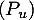 , montrer que
, montrer que 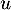 est diagonalisable.
est diagonalisable.
Deuxième partie. Soit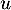 un endomorphisme de
un endomorphisme de 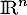 .
.
- Soit
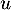 un endomorphisme diagonalisable. Montrer que
un endomorphisme diagonalisable. Montrer que  vérifie
vérifie 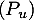 .
.
- Réciproquement, si
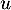 vérifie
vérifie 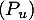 , est-ce que u est diagonalisable ?
, est-ce que u est diagonalisable ?
Correction
Correction
Oral ENS ULM - 2017- Soit
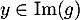 , alors il existe
, alors il existe  tel que
tel que  et on a alors
et on a alors
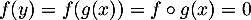 , et donc
, et donc  .
.
On a démontré ainsi que
![\[\text{Im}(g)\subset\ker(f)\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/6.png)
et donc aussi, en particulier, que
![\[rg(g)=\dim\lp\text{Im}(g)\rp\leqslant\dim(\ker(f))\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/7.png)
- D'après le théorème du rang, on a
![\[rg(g)+\dim\lp\ker(g)\rp=\dim\lp\R^n\rp=n\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/8.png)
d'où, avec le résultat de la question précédente,
![\[\dim(\ker(f)) + \dim(\ker(g))\geqslant rg(g)+\dim(\ker(g))=n\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/9.png)
- On peut commencer par étudier l'intersection:
soit
 ,
alors d'une part
,
alors d'une part 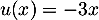 ,
et d'autre part
,
et d'autre part
![\[\left( u-2Id\rp^2(x)=u^2(x)-4u(x)+4x=0\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/12.png)
soit aussi
![\[\begin{array}{lcl}0&=&\left( u-2Id\rp^2(x)\\[.5em]&=&(-3)^2x-4\tm(-3)x+4x\\[.5em]&=&7x\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/13.png)
et donc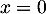 .
.
On peut de plus utiliser la question précédente, avec et
et 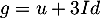 :
:
![\[\dim\lp\ker\lp(u-2Id)^2\rp\rp+\dim\lp\ker(u+3Id)\rp\geqslant n=\dim\lp\R^n\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/17.png)
et donc, est un sous-espace de
est un sous-espace de 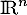 ,
de dimension supérieure à celle de
,
de dimension supérieure à celle de 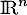 , d'où, nécessairement
, d'où, nécessairement
![\[\ker((u-2Id)^2 )\oplus\ker(u+3Id)=\R^n\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/21.png)
- Si
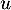 vérifie de plus
vérifie de plus 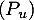 alors, en particluier
alors, en particluier
 et alors
et alors
![\[\begin{array}{lcl}R^n&=&\ker(u-2Id)\oplus\ker(u+3Id)\\[.5em]
&=&E_2(u)\oplus E_{-3}(u)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/25.png)
En d'autres termes, l'espace se décompose en somme directe de sous espaces propres de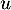 , ce qui montre que
, ce qui montre que  est bien diagonalisable.
est bien diagonalisable.
-
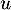 est diagonalisable, donc ses sous-espaces propres sont en somme directe dans
est diagonalisable, donc ses sous-espaces propres sont en somme directe dans 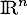 ,
,
![\[\R^n=\underset{\lambda\in SP\la u\ra}{\bigoplus}\ker(u-\lambda Id)\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/30.png)
et en particulier, en prenant les dimensions
![\[n=\sum_{\lambda\in SP\la u\ra}\dim\lp\ker(u-\lambda)\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/31.png)
Supposons qu'il existe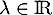 tel que
tel que
![\[\ker(u-\lambda Id)\not=\ker\lp(u-\lambda Id)^2\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/33.png)
et donc, en particulier, comme on a toujours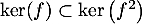 ,
,
![\[\dim\lp\ker(u-\lambda Id)\rp<\dim\lp\ker\lp(u-\lambda Id)^2\rp\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/35.png)
Or, comme à la question 3,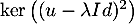 et
et 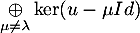 sont en somme directe, soit aussi
sont en somme directe, soit aussi
![\[\dim\lp\ker\lp(u-\lambda Id)^2\rp\rp+\dim\lp\underset{\mu\not=\lambda}{\oplus}\ker(u-\mu Id)\rp\leqslant n\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/38.png)
mais, par ailleurs,
![\[\dim\lp\ker\lp(u-\lambda Id)^2\rp\rp+
\dim\lp\underset{\mu\not=\lambda}{\bigoplus}\ker(u-\mu Id)\right) >
\dim\lp\underset{\mu\in\R}{\bigoplus}\ker(u-\mu Id)\rp=n\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/39.png)
ce qui est impossible: il n'existe donc pas de réel tel que
tel que
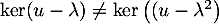 , ce qui signifie que
, ce qui signifie que 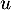 vérifie la propriété
vérifie la propriété  .
.
- Prenons par (contre)exemple l'endomorphisme
 de
de 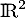 dont la matrice dans la base canonique est
dont la matrice dans la base canonique est
![\[A=\lp\begin{array}{cc}0&1\\1&0\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/46.png)
qui n'admet aucune valeur propre, donc qui n'est pas diagonalisable, et pour lequelle, pour tout réel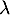 ,
on a
,
on a
![\[\ker(u-\lambda Id)=\ker\lp(u-\lambda Id)^2\rp=\la 0\ra\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago_c/48.png)
puisque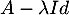 est inversible, donc
est inversible, donc
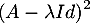 aussi.
aussi.
Tag:Diagonalisation
Autres sujets au hasard:

Voir aussi: