Calculer l'intégrale …
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Calculer l'intégrale
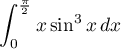
Correction
,
,
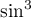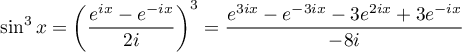et on peut continuer les calculs avec les complexes, en utilisant
![\[\begin{array}{ll}
\dsp\int_0^{\frac\pi2}xe^{\alpha x}\,dx
&\dsp=\Bigl[ \dfrac1\alpha xe^{\alpha x}\Bigr]_0^{\frac\pi2}
-\dfrac1\alpha\int_0^{\frac\pi2}e^{\alpha x}\,dx\\[1em]
&\dsp=\dfrac{\pi}{2\alpha}e^{\frac{\alpha\pi}{2}}
-\dfrac{1}{\alpha^2}\left( e^{\frac{\alpha\pi}{2}}-1\right)
\enar\]](/Generateur-Devoirs/Colles/Integrale/exC5_c/3.png)
… d'où …
![\[\int_0^{\frac\pi2} x\sin^3 x\,dx=\dfrac79\]](/Generateur-Devoirs/Colles/Integrale/exC5_c/4.png)
Correction
Avec la formule d'Euler pour linéariser le,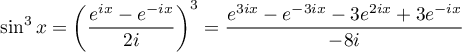
,
et on peut continuer les calculs avec les complexes, en utilisant
… d'où …
Tag:Intégrale
Autres sujets au hasard:
