Base ou non ?
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
On se place dans un espace vectoriel de dimension 3 dont une base est 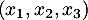 .
.
La famille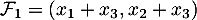 est-elle une base de
est-elle une base de  ?
?
La famille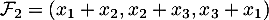 est-elle une base de
est-elle une base de 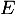 ?
?
Et la famille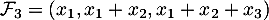 ?
?
La famille
La famille
Et la famille
Correction
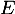 a une base formée de trois vecteurs. Il est donc de dimension 3.
a une base formée de trois vecteurs. Il est donc de dimension 3.
La famille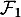 n'est formée que de deux vecteurs, et donc
n'est formée que de deux vecteurs, et donc
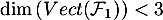 et cette famille ne peut pas être génératrice de
et cette famille ne peut pas être génératrice de 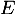 . En particulier, cette famille ne peut pas être une base.
. En particulier, cette famille ne peut pas être une base.
Les deux autres familles possèdent le bon nombre de vecteurs pour former une base de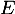 , encore faut-il qu'elles soient libres.
, encore faut-il qu'elles soient libres.
Pour le vérifier, on considère une combinaison linéaire nulle des vecteurs de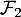 :
:
![\[a(x_1+x_2)+b(x_2+x_3)+c(x_3+x_1)=0\]](/Generateur-Devoirs/Colles/ev/exbases_c/7.png)
Cette combinaison linéaire s'écrit aussi en réordonnant
![\[(a+c)x_1+(a+b)x_2+(b+c)x_3)=0\]](/Generateur-Devoirs/Colles/ev/exbases_c/8.png)
Comme la famille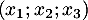 est libre (car c'est une base), cette dernière combinaison linéaire est nulle si et seulement si
est libre (car c'est une base), cette dernière combinaison linéaire est nulle si et seulement si
![\[\la\begin{array}{rcrcl}
a&+&c&=&0\\
a&+&b&=&0\\
b&+&c&=&0\enar\right.\]](/Generateur-Devoirs/Colles/ev/exbases_c/10.png)
En soustrayant les deux premières équations on trouve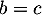 , puis de même avec les deux dernières on trouve
, puis de même avec les deux dernières on trouve  . Ainsi
. Ainsi 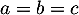 et alors la première équation s'écrit
et alors la première équation s'écrit 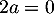 soit
soit  et donc finalement
et donc finalement 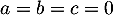 .
.
On vient donc de montrer que la famille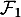 est libre et qu'elle forme donc aussi une base de
est libre et qu'elle forme donc aussi une base de 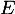 .
.
On procède de même pour la troisième famille, soit trois coefficients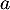 ,
, 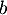 et
et 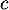 qui annulent la combinaison linéaire:
qui annulent la combinaison linéaire:
![\[ax_1+b(x_1+x_2)+c(x_1+x_2+x_3)=0\]](/Generateur-Devoirs/Colles/ev/exbases_c/22.png)
soit aussi, en réordonnant,
![\[(a+b+c)x_1+(b+c)x_2+cx_3=0\]](/Generateur-Devoirs/Colles/ev/exbases_c/23.png)
et comme famille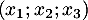 est libre (car c'est une base), cette dernière combinaison linéaire nulle implique nécessairement que
est libre (car c'est une base), cette dernière combinaison linéaire nulle implique nécessairement que
![\[\la\begin{array}{rcrcrcl}
a&+&b&+&c&=&0\\
&&b&+&c&=&0\\
&&&&c&=&0\enar\right.\]](/Generateur-Devoirs/Colles/ev/exbases_c/25.png)
Ce système triangulaire se résout très facilement en commençant par la dernière équation, et on trouve que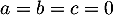 .
.
Ainsi, la famille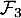 est libre et c'est donc une base de
est libre et c'est donc une base de 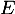
Correction
L'espaceLa famille
Les deux autres familles possèdent le bon nombre de vecteurs pour former une base de
Pour le vérifier, on considère une combinaison linéaire nulle des vecteurs de
Cette combinaison linéaire s'écrit aussi en réordonnant
Comme la famille
![\[\la\begin{array}{rcrcl}
a&+&c&=&0\\
a&+&b&=&0\\
b&+&c&=&0\enar\right.\]](/Generateur-Devoirs/Colles/ev/exbases_c/10.png)
En soustrayant les deux premières équations on trouve
On vient donc de montrer que la famille
On procède de même pour la troisième famille, soit trois coefficients
soit aussi, en réordonnant,
et comme famille
![\[\la\begin{array}{rcrcrcl}
a&+&b&+&c&=&0\\
&&b&+&c&=&0\\
&&&&c&=&0\enar\right.\]](/Generateur-Devoirs/Colles/ev/exbases_c/25.png)
Ce système triangulaire se résout très facilement en commençant par la dernière équation, et on trouve que
Ainsi, la famille
Tag:Espace vectoriel
Autres sujets au hasard:

Voir aussi: