Variables aléatoires
Loi de probabilités - Espérance, variance et écart-type
Rappels, échauffement …
Exercice 1: Comparer des résultats
Deux élèves ont eu les notes suivantes:- Élève A:
- 9; 10; 15; 17; 11; 5; 3; 10
- Élève B:
- 9; 10; 11; 10; 9; 10; 11; 10
- Élève C:
- 12; 13; 9; 10; 9; 8; 9; 10
Correction
La moyenne de chacun de ces élèves est la même: 10.
Donner la moyenne est insuffisant pour comparer des séries statistiques.
On complète pour cette raison la moyenne par un autre indicateur: l'écart-type.
Exercice 2: un jeu avantageux ?
Un jeu consiste à lancer deux fois de suite une pièce de monnaie bien équilibrée.
Pour jouer à ce jeu on mise 2 euros. Lorsqu'on obtient deux fois pile, on gagne 6 euros, et on gagne 3 euro pour deux fois face. Dans tous les autres cas, on ne gagne rien et on perd notre mise.
Représenter la situation à l'aide d'un arbre, et remplir un tableau des gains et de leur probabilité.
Ce jeu semble-t-il avantageux pour le joueur ? Combien gagne-t-il, ou perd-il, en moyenne sur une partie ?
Correction
On représente la situation grâce à l'arbre suivant, dans lequel on note les probabilités ainsi que les gains correspondants à chaque cehmin:

- Obtenir un gain de 4 euros: la probabilité est de 12×12=14
- Obtenir un gain de 1 euro: la probabilité est de 12×12=14
- Obtenir un gain de −2 euros (donc perdre 2 euros): la probabilité est de 12×12+12×12=12
| Gains | 4 | 1 | −2 |
| Probabilités | 14 | 14 | 12 |
En particulier, en moyenne, le gain est de
4×14
+ 1×14
+(−2)×12
14+12+14
= 14
Ce gain est positif et le jeu est donc favorable au joueur.
Ce jeu, et ses gains (ou pertes), peut être simulé à la page: simulation et fluctuation des résultats aléatoires.
Variables aléatoires
Définition: variable aléatoire
Soit Ω l'ensemble des issues d'une expérience aléatoire.
Une variable aléatoire sur Ω est une fonction définie sur Ω à valeur dans R.
Exemple: Dans l'exercice 2, l'univers est Ω = { PP ; PF; FP; FF }, et on définit la variable aléatoire X qui prend les valeurs x1 = 3, x2 = 1 et x3 = −2.
| Événement | PP | FF | PF; FP |
| xi | 3 | 1 | −2 |
Dans ce jeu, les probabilités nous intéressent particulièrement car il s’agit d'un jeu (ou une expérience) aléatoire:
| Événement | PP | FF | PF; FP |
| xi | 3 | 1 | −2 |
| Probabilités | 1/4 | 1/4 | 1/2 |
Définition: Loi de probabilité
Soit X une variable aléatoire définie sur Ω.
La loi de probabilité de la variable aléatoire X est l'ensemble des probabilités des événements {X = xi} pour chaque valeur xi prise par X:
| xi | x1 | x2 | … | xn |
| P(X=xi) | p1 | p2 | … | pn |
Exercice 3: QCM
Lors d'un examen, un élève doit répondre à un QCM.
Ce QCM comporte trois questions et, pour chaque question, trois réponses différentes sont proposées, dont une seule est exacte.
- Représenter toutes les issues possibles à l'aide d'un arbre.
- Chaque réponse exacte rapporte 1 point, chaque réponse fausse enlève 0,5 point.
Une note totale négative est ramenée à 0.
On appelle X le total des points que l'élève a obtenu pour cet exercice.
Déterminer les différentes valeurs prises par X, et donner le tableau de la loi de probabilité de X.
Correction
- On représente la situation avec un arbre de probabilités.
Il y 3 questions, et à chaque question, on répond soit juste (J), soit Faux (F).
On suppose que les réponses données à chaque question sont indépendantes de celles données aux autres questions.
![\[\psset{xunit=1cm,yunit=1.5cm}
\begin{pspicture}(-.2,-2.5)(6.2,1.4)
\psline(0,0)(1.5,1)\rput(1.75,1){$J$}\rput(.6,.7){$\frac13$}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$F$}
\rput(.6,-.8){$\frac23$}%
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$J$}\rput(2.8,1.7){$\frac13$}
\psline(2.1,.8)(3.5,.5)\rput(3.8,.5){$F$}\rput(2.8,.5){$\frac23$}%
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$F$}\rput(2.8,-1.6){$\frac23$}
\psline(2.1,-.8)(3.5,-.5)\rput(3.8,-.5){$J$}\rput(2.8,-.5){$\frac13$}%
\psline(4.1,1.6)(5.5,1.4)\rput(5.8,1.4){$F$}\rput(4.8,1.3){$\frac23$}
\psline(4.1,1.6)(5.5,1.8)\rput(5.8,1.8){$J$} \rput(4.8,1.9){$\frac13$}%
\psline(4.1,.5)(5.5,.75)\rput(5.8,.75){$J$}\rput(4.8,.85){$\frac13$}
\psline(4.1,.5)(5.5,.25)\rput(5.8,.25){$F$} \rput(4.8,.2){$\frac23$}%
\psline(4.1,-.5)(5.5,-.75)\rput(5.8,-.75){$F$}\rput(4.8,-.85){$\frac23$}
\psline(4.1,-.5)(5.5,-.25)\rput(5.8,-.25){$J$} \rput(4.8,-.2){$\frac13$}%
\psline(4.1,-1.6)(5.5,-1.4)\rput(5.8,-1.4){$J$}\rput(4.8,-1.3){$\frac13$}
\psline(4.1,-1.6)(5.5,-1.8)\rput(5.8,-1.8){$F$} \rput(4.8,-1.9){$\frac23$}
\end{pspicture}\]](./arbre-QCM.png)
- On ajoute de plus à cette arbre la note correspondante, notée X, obtenue à chaque chemin.
{$\to X=1,5$}
\psline(4.1,1.6)(5.5,1.8)\rput(5.8,1.8){$J$} \rput(4.8,1.9){$\frac13$}
\rput[l](6.1,1.8){$\to X=3$}%
\psline(4.1,.5)(5.5,.75)\rput(5.8,.75){$J$}\rput(4.8,.85){$\frac13$}
\rput[l](6.1,.75){$\to X=1,5$}
\psline(4.1,.5)(5.5,.25)\rput(5.8,.25){$F$} \rput(4.8,.2){$\frac23$}
\rput[l](6.1,.25){$\to X=0$}%
\psline(4.1,-.5)(5.5,-.75)\rput(5.8,-.75){$F$}\rput(4.8,-.85){$\frac23$}
\rput[l](6.1,-.75){$\to X=0$}
\psline(4.1,-.5)(5.5,-.25)\rput(5.8,-.25){$J$} \rput(4.8,-.2){$\frac13$}
\rput[l](6.1,-.25){$\to X=1,5$}%
\psline(4.1,-1.6)(5.5,-1.4)\rput(5.8,-1.4){$J$}\rput(4.8,-1.3){$\frac13$}
\rput[l](6.1,-1.4){$\to X=0$}
\psline(4.1,-1.6)(5.5,-1.8)\rput(5.8,-1.8){$F$} \rput(4.8,-1.9){$\frac23$}
\rput[l](6.1,-1.8){$\to X=0$}
\end{pspicture}\]](./arbre-QCM-variable-aleatoire.png)
La variable aléatoire X peut donc prendre 3 valeurs: 3; 1,5 et 0, pour lesquelles on peut calculer les probabilités (en utilisant les règles d'utilisation des arbres de probabilité):- Probabilité d'obtenir 3 points:
P(X=3) = 13×13×13=133=127
- Probabilité d'obtenir 1,5 points:
P(X=1,5) = 13×13×23 + 13×23×13 + 23×13×13 = 3×13×13×23 =29
- Probabilité d'obtenir 0. On peut soit calculer la probabilité comme précédemment, soit utilisr le fait que la somme des probabilités vaut 1, soit
P(X=0) + P(X=1,5) + P(X=3 )= 1et doncP(X=0) = 1 − P(X=1,5) − P(X=3)d'oùP(X=0) = 1 − 127 − 29 = 2027
xi 3 1,5 0 P(X=xi) 127 29 2027 - Probabilité d'obtenir 3 points:
Espérance d'une variable aléatoire
Définition: espérance
Soit X une variable aléatoire de loi de probabilité:
| xi | x1 | x2 | … | xn |
| pi = P(X=xi) | p1 | p2 | … | pn |
E(X)
=
n∑i=1pixi
= p1x1 + p1x1 + … + pnxn
L'espérance est la moyenne des valeurs prises par X, moyenne pondérée par les probabilités.
Exercice 4
Calculer l'espérance de la variable aléatoire X dont la loi de probabilité est:
| xi | −2 | 0 | 1 | 3 |
| pi = P(X=xi) | 0,4 | 0,2 | 0,3 | 0,1 |
On calcule l'espérance:
E(X) =
−2×0,4 + 0×0,2 + 1×0,3 + 3×0,1
= −0,2
Exercice 5
On donne la loi de probabilité d'une variable aléatoire X:
| xi | −2 | a | 3 |
| pi = P(X=xi) | 0,4 | 0,2 | 0,3 |
L'expression de l'espérance est
E(X) = −2×0,4 + a×0,2 + 3×0,3
= 0,1 + 0,2a
et on veut donc E(X)=2, soit
0,1 + 0,2a = 2 ⇔ a =
1,90,2= 9,5
Exercice 6
Donner l'espérance du QCM de l'exercice 3
On avait la loi de probabilité
et donc l'espérance
| xi | 3 | 1,5 | 0 |
| P(X=xi) | 127 | 29 | 2027 |
E(X) = 3×127
+ 1,5×29
+ 0×2027
= 49
Exercice 7
Une société d'assurance classe les sinistres en trois catégories, A, B et C, pour lesquelles une étude statistique, parmi ses assurés, a établi les probabilités:
P(A) = 0,2, P(B) = 0,1 et P(C) = 0,02.
Pour les victimes de ces sinistres, la société d'assurance rembourse respectivement 100 euros, 500 euros et 1500 euros.
Les assurés auprès de cette assurance paient tous la même cotisation annuelle.
On note X la variable aléatoire égale à la différence entre la cotisation et le remboursement.
Quel doit être le montant de la cotisation pour avoir E(X) = 0.
On note c la cotisation payées par les assurés.
On a alors la loi de probabilité
et l'espérance:
On a alors la loi de probabilité
| xi | c−100 | c−500 | c−1500 |
| P(X=xi) | 0,2 | 0,1 | 0,02 |
E(X) = (c−100)×0,2
+ (c−500)×0,1 + (c−1500)×0,02
= 0,32c − 100
et l'espérance est donc nulle pour une cotisation
E(X) = 0,32c − 100 = 0
⇔ c = 1000,32
= 312,5
Exercice 8
Une usine fabrique des objets destinés à êetre commercialisés. Les objets fabriqués peuvent éventuellement avoir deux défauts, le défaut A et le défaut B.
On estime que, en moyenne à la sortie de cette usine, 15% des objets ont le défaut A, 7% ont le défaut B, et 3% ont les deux défauts à la fois.
Le coût de production d'un objet est de 30 euros. La réparation du défaut A revient à 5 euros, et la réparation du défaut B revient à 8 euros.
-
- Quel est le pourcentage d'objets défectueux (c'est-à-dire ayant au moins un défaut) ?
- J'ai pris un objet à la sortie de cette usine et je m'aperçois qu'il a le défaut A. Quelle est la probabilité qu'il ait aussi le défaut B.
- On note X la variable aléatoire qui associe à un objet au hasard de la production son coût: fabrication et réparations éventuelles.
- Déterminer la loi de probabilité de X.
- Calculer E(X) et interpréter la valeur trouvée.
- On suppose que tous les objets fabriqués sont vendus.
Quel doit être le prix de vente de chaque objet pour que l'usine réalise un bénéfice de 20 euros par objet ?
-
- L'ensemble des objets défectueux est la réunion de ceux ayant le défaut A et ceux ayant le défaut B; leur pourcentage est de:
P(A∪B) = P(A) + P(B) − P(A∩B)soit la proportionP(A∪B) = 15% + 7% − 3% = 19%
- On cherche la probabilité conditionnelle:
PA(B) = P(A∩B)P(A) = 3%15% = 0,2%
- L'ensemble des objets défectueux est la réunion de ceux ayant le défaut A et ceux ayant le défaut B; leur pourcentage est de:
-
- Il y a 4 possibilités: la pièce prise au hasard
- a les deux défauts, alors X=30+5+8=43, de probabilité P(A∩B)=3%
- n'a aucun défaut, alors X=30%, de probabilité 100%−P(A∪B)=81%
- a le défaut A exclusivement, alors X=30+5=35, de probabilité 15%−3%=12%
- a le défaut B exclusivement, alors X=30+8=38, de probabilité 7%−3%=4%
xi 30 35 38 43 P(X=xi) 81% 12% 4% 3% - On calcule alors l'espérance
E(X) = 30×81% + 35×12% + 38×4% + 43×3% = 31,31
- Il faut donc chaque objet 20 euros plus cher, soit 51,31 euros.
- Il y a 4 possibilités: la pièce prise au hasard
Propriété: Linéarité de l'espérance
Pour tous réels a et b, on a
E(aX+b) = aE(X) + b
Exercice 9
Pour me rendre au travail, je prends le bus. Le trajet comporte 4 arrêts; le bus ne s'y arrête pas forcément, ce qui rend mon trajet plus ou moins rapide.
On note S le nombre d'arrêts que le bus fait effectivement. Une étude statistique montre que la loi de probabilité de S est
| xi | 0 | 1 | 2 | 3 | 4 |
| P(S=xi) | 0,05 | 0,15 | 0,3 | 0,35 | 0,15 |
- Calculer P(S≥3) et interpréter dans le contexte de l'exercice.
- Calculer E(S) et interpréter ce résultat.
- Le trajet direct, sans arrêt, dure 20 minutes. Chaque arrêt prend 3 minutes.
On note T la variable aléatoire égale à la durée du trajet.- Quelle relation lie S et T ?
- Déterminer le temps de trajet moyen pour me rendre à mon travail.
- Je monte dans le bus et j'ai 25 minutes pour arriver à mon travail à l'heure. Quelle est la probabilité que je sois en retard ?
- P(S≥3) = P(S=3) + P(S=4) = 0,35 + 0,15 = 0,5
- E(S) = 0×0,05 + 1×0,15 + 2×0,3 + 3×0,35 + 4×0,15 = 2,4
En moyenne, sur un grand nombre de trajets, le bus s'arrête 2,4 fois. -
- T = 20 + 3S
- Le temps de trajet moyen est alors, en utilisant la propriété précédente de linéarité de l'espérance
E(T) = E(20 + 3S) = E(20) + 3E(S)et donc, comme E(20)=20, on obtientE(T) = 20 + 3×2,4 = 27,2
- On complète le tableau de la loi de probabilité de S pour donner celle de T
La probabilité que j'arrive en retard est alorsxi 0 1 2 3 4 ti 20 23 26 29 32 P(S=xi) 0,05 0,15 0,3 0,35 0,15 P(T>25) = P(T=26) + P(T=29) + P(T=32) = 0,8
Variance et écart-type d'une variable aléatoire
Définition: Variance et écart-type
- La variance de la variable aléatoire X est le nombre
E(X) = n∑i=1pi (xi − E(X))2 = p1(x1−E(X))2 + … + pn(xn−E(X))2
- L'écart-type de X est le nombre σ(X) = V(X)
Exercice 10
Calculer la variance et l'écart-type de la variable aléatoire de l'exercice 4.
Exercice 11
Calculer l'espérance, la variance et l'écart-type de la variable aléatoire Y dont la loi de probabilité est:
| xi | −3 | −1 | 0 | 2 | 5 |
| P(Y=xi) | 0,2 | 0,1 | 0,4 | 0,25 | 0,05 |
Propriété
Pour X une variable aléatoire et a et b deux réels, on a
V(aX+b) = a2V(X)
et donc
σ (aX+b) = |a| σ (X)
Exercice 12
On considère la variable aléatoire N dont la loi de probabilité est:
| xi | 2 | 3 | 5 | 8 |
| P(Y=xi) | 0,1 | 0,35 | 0,4 | 0,15 |
- Calculer l'espérance, la variance et l'écart-type de N.
- Les valeurs de N sont en fait les notes obtenues à un devoir noté sur 8.
Pour ramener ces notes sur 20, le professeur décide de simplement multiplier chaque note par 2 et d'y ajouter ensuite 4 points.
Déterminer l'espérance, variance et écart-type de ces nouvelles notes.
Exercices
Exercice 13: service de dépannage téléphonique.
Un client cherche à joindre par téléphone un service de dépannage.
La probabilité que son appel soit pris sans attente est de 0,25.
Si son appel n'est pas pris sans attente, le client raccroche son téléphone et fait une autre tentative.
Le client fait au maximum trois tentatives.
On note X la variable aléatoire égale au rang de son premier appel aboutissant sans attente. Si au bout de trois appels le client n'a pas réussi à joindre le service de dépannage sans attente, on convient alors que X = 0.
On note R l'événement: "Le client est mis en relation avec le service de dépannage sans attente."
- Représenter la situation par un arbre de probabilités.
- Quelles valeurs peut prendre la variable aléatoire X ?
Déterminer alors la loi de probabilité de X. - Déterminer l'espérance de la variable aléatoire X, et interpréter ce résultat.
-
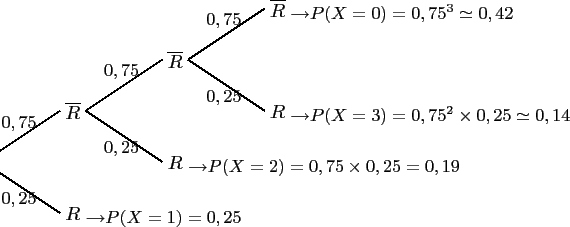
- La variable aléatoire X peut être égale à:
0; 1; 2 ou 3.
k 0 1 2 3 P(X=k) 0,42 0,25 0,19 0,14 -
E(X)≃0× 0,42 + 1× 0,25 + 2× 0,19 + 3× 0,14 ≃1,05
En moyenne, le client joindra le service clientèle en un peu plus d'un appel.
Exercice 14: Politique de naissances.
Dans un pays fictif, on impose la loi de naissance suivante : chaque couple peut avoir au maximum trois enfants et ne peut avoir qu'un seul garçon.
On suppose que les probabilités de naissance garçon/fille sont égales, et que tout le monde respecte la loi (et donc ne cherche plus à avoir d'enfant après la naissance d'un garçon).
On note X la variable aléatoire égale au nombre d'enfants qu'a un couple, et F et G le nombre de filles et de garçons.
À l'aide d'un arbre de probabilité, donner les lois de probabilités de X, F et G.
En déduire E(X), E(F) et E(G). Commenter.
On représente la situation par un arbre de probabilité, qui est donc tronqué à chaque naissance de garçon:
![\[\psset{xunit=1cm,yunit=1.5cm}
\begin{pspicture}(-.2,-2.5)(6.2,1.4)
\psline(0,0)(1.5,.5)\rput(1.75,.5){$G$}\rput(.6,.42){$\frac12$}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$F$}
\rput(.6,-.7){$\frac12$}%
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$F$}\rput(2.8,-1.6){$\frac12$}
\psline(2.1,-.8)(3.5,-.5)\rput(3.8,-.5){$G$}\rput(2.8,-.5){$\frac12$}%
\psline(4.1,-1.6)(5.5,-1.4)\rput(5.8,-1.4){$G$}\rput(4.8,-1.3){$\frac12$}
\psline(4.1,-1.6)(5.5,-1.8)\rput(5.8,-1.8){$F$} \rput(4.8,-1.9){$\frac12$}
\end{pspicture}\]](./arbre-naissances-GF.png)
On dresse alors les tableaux donnant les lois de probabilité pour les nombres de garçons et de filles:
Pour les garçons, il n'y a que deux cas, ne pas en avoir ou en avoir 1 seul (qui est alors l'événement contraire):
et enfin, pour le nombre d'enfants:
et on peut calculer les espérances:
De même
Remarque: On retrouve (ou on aurait pu utiliser aussi) par linéarité de l'espérance: E(X)=E(X+Y) = E(X) + E(Y)
De plus, ces calculs montrent que le nombre de garçons et de filles par famille restent les mêmes, malgré cette politique imposée de naissance, qui ne change donc pas globalement la répartition garçon/fille.
![\[\psset{xunit=1cm,yunit=1.5cm}
\begin{pspicture}(-.2,-2.5)(6.2,1.4)
\psline(0,0)(1.5,.5)\rput(1.75,.5){$G$}\rput(.6,.42){$\frac12$}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$F$}
\rput(.6,-.7){$\frac12$}%
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$F$}\rput(2.8,-1.6){$\frac12$}
\psline(2.1,-.8)(3.5,-.5)\rput(3.8,-.5){$G$}\rput(2.8,-.5){$\frac12$}%
\psline(4.1,-1.6)(5.5,-1.4)\rput(5.8,-1.4){$G$}\rput(4.8,-1.3){$\frac12$}
\psline(4.1,-1.6)(5.5,-1.8)\rput(5.8,-1.8){$F$} \rput(4.8,-1.9){$\frac12$}
\end{pspicture}\]](./arbre-naissances-GF.png)
On dresse alors les tableaux donnant les lois de probabilité pour les nombres de garçons et de filles:
| k | 0 | 1 | 2 | 3 |
| P(F=k) | 12 | 12×12=14 | 12×12×12=18 | 12×12×12=18 |
| k | 0 | 1 |
| P(G=k) | 12×12×12=18 | 1−18=78 |
| k | 1 | 2 | 3 |
| P(X=k) | 12 | 12×12=14 | 14 |
E(X) = 1×12
+ 2×14
+ 3×14
= 74
ce qui signifie que, en moyenne sur un grand nombre de familles, le nombre moyen d'enfants par famille est un peu inférieur à 2 (1,75).
De même
E(G) = 0×18
+ 1×78
= 78
et
E(F) = 0×12
+ 1×14
+ 2×18
+ 3×18
= 78
Remarque: On retrouve (ou on aurait pu utiliser aussi) par linéarité de l'espérance: E(X)=E(X+Y) = E(X) + E(Y)
De plus, ces calculs montrent que le nombre de garçons et de filles par famille restent les mêmes, malgré cette politique imposée de naissance, qui ne change donc pas globalement la répartition garçon/fille.
Exercice 15: chance de gagner à un jeu
Un jeu de hasard sur ordinateur est conçu de la façon suivante:
- Si le joueur gagne une partie, la probabilité qu'il gagne la partie suivante est 14
- Si le joueur perd une partie, la probabilité qu'il perde la partie suivante est 12
- La probabilité de gagner la première partie est 14
On a donc en particulier p1 = 14
- Montrer que p2 = 716
- Montrer que, pour tout entier naturel n, on a pn+1 = −14pn + 12
- On définit, pour tout entier naturel n non nul, la suite (un) par
un = pn−25
- Démontrer que la suite (un) est une suite géométrique dont on précisera la raison.
- En déduire que, pour tout entier naturel n non nul, on a
pn = 25 − 320−14n−1
- On représente la situation par un arbre de probabilité:
![\[\psset{xunit=1.cm,yunit=.8cm}
\begin{pspicture}(0,-5.)(5,2)
\psline(0,0)(1.4,1.5)\rput(1.75,1.5){$G_1$}\rput(0.7,1.2){$\frac14$}
\psline(2,1.5)(3.4,2.25)\rput(3.75,2.25){$G_2$}\rput(2.7,2.2){$\frac14$}
\psline(2,1.5)(3.4,0.75)\rput(3.75,0.75){$\overline{G_2}$}\rput(2.7,0.7){$\frac34$}
%
\psline(0,0)(1.4,-1.5)\rput(1.75,-1.5){$\overline{G_1}$}\rput(0.7,-1.2){$\frac34$}
\psline(2,-1.5)(3.4,-0.75)\rput(3.75,-0.75){$G_2$}\rput(2.7,-0.7){$\frac12$}
\psline(2,-1.5)(3.4,-2.25)\rput(3.75,-2.25){$\overline{G_2}$}\rput(2.7,-2.2){$\frac12$}
\end{pspicture}\]](./arbre-jeu-G1-G2.png)
et on a alors, en utilisant cet arbre et la formule des probabilités totales:p2 = P(G2) = 14×14 + 34×12 = 716 - On reprend l'arbre précédent, mais pour la n-ième partie:
{$G_{n+1}$}\rput(2.7,2.2){$\frac14$}
\psline(2,1.5)(3.4,0.75)\rput[l](3.5,0.75){$\overline{G_{n+1}}$}\rput(2.7,0.7){$\frac34$}
%
\psline(0,0)(1.4,-1.5)\rput(1.75,-1.5){$\overline{G_n}$}\rput(0.7,-1.2){$\frac34$}
\psline(2,-1.5)(3.4,-0.75)\rput[l](3.5,-0.75){$G_{n+1}$}\rput(2.7,-0.7){$\frac12$}
\psline(2,-1.5)(3.4,-2.25)\rput[l](3.5,-2.25){$\overline{G_{n+1}}$}\rput(2.7,-2.2){$\frac12$}
\end{pspicture}\]](./arbre-jeu-Gn.png)
et on a alors, en utilisant cet arbre et la formule des probabilités totales:pn+1 = P(Gn+1) = pn×14 + (1−pn)×12soit finalementpn+1 = −14pn + 12 -
- Pour tout entier n, on a
un+1 = pn+1−25soit, en utilisant l'expression trouvée à la question précédente,un+1 = −14pn + 12 −25 = −14pn + 110et donc, en factorisant,un+1 = −14 pn − 25 = −14unce qui montre que la suite (un) est géométrique de raison q = −14
-
On en déduit que, pour tout entier n≥1, on a
un = u1qn−1avecu1 = p1 −25 = 14 −25 = −320et alorsun = u1qn−1 = −320−14n−1et enfin, commeun = pn−25 ⇔ pn = un + 25on trouve le résultat recherché:pn = 25 − 320−14n−1
- Pour tout entier n, on a
Exercice 15: Tirage de cartes: quand s'arrêter ?
Un joueur pioche dans un jeu de 52 cartes autant de cartes qu'il le désire sans les regarder.
Une fois qu'il décide de s'arrêter, il prend connaissance de toutes les cartes qu'il a pioché. Si parmi elle, il a tiré l'as de pique, il perd 10 euros. Sinon, il gagne 1 euro par carte tirée.
Combien doit-il piocher de cartes pour maximiser son gain moyen ? Combien peut-il alors espérer gagner ?
On note X le gain algébrique d'une partie. Soit X=−10 si l'as de pique a été tiré, sinon X=n où n est le nombre de cartes qui ont été tirées.
Pour n cartes tirées au hasard, la probabilité d'y avoir l'as de pique est de n52 et donc, la probabilité que l'as de pique n'y soit pas est de 1− n52
On a ainsi la loi de probabilité de X pour n cartes tirées, pour 1≤n≤52:
Il reste maintenant à calculer l'espérance de ce gain, afin de chercher ensuite à le maximiser:
L'espérance est alors, avec n=21,
Pour n cartes tirées au hasard, la probabilité d'y avoir l'as de pique est de n52 et donc, la probabilité que l'as de pique n'y soit pas est de 1− n52
On a ainsi la loi de probabilité de X pour n cartes tirées, pour 1≤n≤52:
| xi | −10 | n |
| P(X=xi) | n52 | 1−n52 |
E(X) = −10×n52
+ n1−n52
soit, sur le même dénominateur,
E(X) =
−n2 + 42n52
L'expression du numérateur est un trinôme du second degré qui atteint son maximum en
α=−b2a
= −42−2 = 21
Le nombre optimal de cartes à tirer est donc de 21 cartes.
L'espérance est alors, avec n=21,
E(X)
= −212 + 42×2152
≃ 8,48
Exercice 17: Loi de Poisson - Exponentielle
Au 19ème siècle, Denis Poisson publie son livre "Recherches sur la probabilité des jugments en matière criminelle et en matière civile" dans lequel il aborde une nouvelle loi de probabilité, qui restera connue par la suite comme la "loi de Poisson".
Pour un réel λ>0, une variable aléatoire X suit la loi de Poisson de paramètre λ lorsque, pour tout entier k naturel, P(X=k) = e−λ λkk! où k! est le produit de tous les entiers de 1 à k (par exemple, 4! = 1×2×3×4 et on précise que, par convention, 0!=1).
- On suppose dans cette question que λ = 0,1. Calculer les probabilités P(X=2) et P(X≤2).
- On considère deux variables aléatoires X et Y indépendantes qui suivent chacune une loi de Poisson de paramètres respectifs λ et μ.
- Calculer P(X+Y=0).
- Calculer de même P(X+Y=1) et P(X+Y=2).
- Quelle loi semble suivre la variable aléatoire X+Y ?
-
P(X=2) = e−0,1
0,122
≃ 0,0045
et P(X=3) = e−0,1 0,132×3 ≃ 0,00015 - X et Y ne peuvent prendre que des valeurs entières.
En particulier X+Y=0 n'est possible que pour X=Y=0, et on a alors
P(X+Y=0)=P((X=0)∩(Y=0))et alors, par indépendance des deux variables aléatoiresP(X+Y=0)=P(X=0)×P(Y=0)avecP(X=0) = e−λλ00! = e−λ11 = e−λet de mêmeP(Y=0) = e−μd'oùP(X+Y=0) = e−λe−μ = e−(λ+μ)
- Il y a ya deux façon d'obtenir l'événement X+Y=1, à savoir d'une part
X=1 et Y=0 et d'autre part
X=0 et Y=1.
On a alorsP(X+Y=1) = P((X=1)∩(Y=0)) + P((X=0)∩(Y=1))et à nouveau, par indépendance des deux variablesP(X+Y=1) = P(X=1)×P(Y=0) + P(X=0)×P(Y=1)Il reste à exprimerP(X=1) = e−λλ11! = e−λλet de mêmeP(Y=1) = eμλμd'où, en utilisant aussi les résultats de la question précédente,P(X+Y=1) = e−λλe−μ + e−λe−μμsoit encoreP(X+Y=1) (λ+μ)e−(λ+μ)
On raisonne encore de la même façon pour X+Y=2 qui se décompose maintenant en 3 événements: X=2 et Y=0, et X=1 et Y=1, et enfin X=0 et Y=2 et, comme précédemment, on a alors queP(X+Y=2) = P(X=2)×P(Y=0) + P(X=1)×P(Y=1) + P(X=0)×P(Y=2)soit, en détaillant chaque terme,P(X+Y=2) = e−λλ22!e−μ + e−λλe−μμ + e−λe−λμ22!En factorisant on obtient alorsP(X+Y=2) = 12e−λe−μ(λ2+2λμ+μ2)et on y trouve une identité remarquable, et avec les règles de calcul algèbrique sur l'exponentielle, on trovue finalement,P(X+Y=2) = 12e−(λ+μ)(λ+μ)2 - La variable X+Y semble donc suivre une loi de poisson de paramètre λ+μ.
Voir aussi: