Variation d'un polynome de degré 3 et équation de la tangente
Exercice corrigé - Spécialité maths, première générale
On considère la fonction  définie sur
définie sur 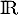 par
par
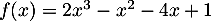 , et on note
, et on note 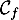 sa courbe représentative.
sa courbe représentative.
- Déterminer la fonction dérivée
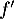 de
de 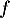 ,
puis dresser le tableau de variation de
,
puis dresser le tableau de variation de 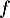 .
.
- Donner l'équation de la tangente à
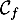 au point d'abscisse 1.
au point d'abscisse 1.
Correction
Cacher la correction
-
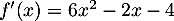 est un trinôme du second degré de discriminant
est un trinôme du second degré de discriminant 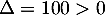 et admet donc deux racines
et admet donc deux racines 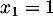 (qui était aussi évidente) et
(qui était aussi évidente) et 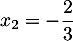 et on a donc
et on a donc
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-2/3$ && 1 && $+\infty$ \\\hline
$6x^2-2x-4$ &&$+$&\zb&$-$&\zb&$+$&\\\hline
&&&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvartgt_c/5.png)
- La tangente en
 a pour équation
a pour équation
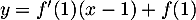 soit, avec
soit, avec 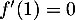 et
et 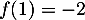 , on obtient l'équation de la tangente (horizontale):
, on obtient l'équation de la tangente (horizontale): 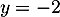 .
.
Cacher la correction
Tag:Fonctions et dérivées
Voir aussi:
