Tangente à une hyperbole
Exercice corrigé - Spécialité maths, première générale
Tangente à une hyperbole
Soit ![]() la fonction inverse:
la fonction inverse:
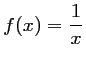 et
et
![]() sa courbe représentative.
sa courbe représentative.
- Déterminer les coordonnées du point
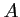 de
de
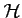 d'abscisse
d'abscisse
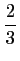 ,
puis une équation de la tangente
,
puis une équation de la tangente 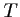 à
à
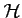 en ce point.
en ce point.
- Déterminer les coordonnées des points
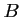 et
et 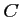 intersections
de
intersections
de 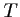 avec les axes de coordonnées.
avec les axes de coordonnées.
Vérifier que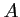 est le milieu de
est le milieu de ![$ [BC]$](/Generateur-Devoirs/1S/Chap3/ex7_img9.png) .
.
- Généralisation: reprendre les questions précédentes avec le
point
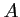 d'abscisse
d'abscisse 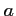 .
.
- Question bonus: en déduire une méthode géométrique de la
construction des tangentes à
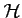 .
.
Correction
Cacher la correction
- Les coordonnées de
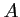 sont
sont
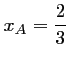 et
et
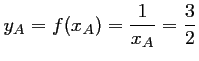 .
.
- On a
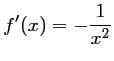 .
L'équation de
.
L'équation de 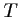 , tangente à
, tangente à
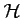 en
en 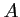 , est:
, est:
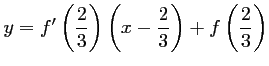 .
.
Comme
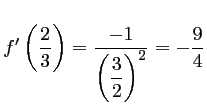 ,
et,
,
et,
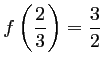 ,
l'équation s'écrit:
,
l'équation s'écrit:
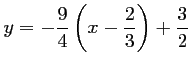 ,
soit
,
soit
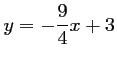 .
.
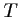 coupe l'axe des abscisses en
coupe l'axe des abscisses en
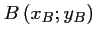 avec
avec 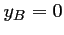 ,
d'où
,
d'où
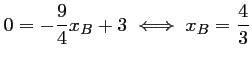 ,
et ainsi,
,
et ainsi,
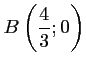 .
.
De même,
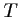 coupe l'axe des ordonnées en
coupe l'axe des ordonnées en
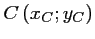 avec
avec
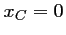 ,
d'où
,
d'où
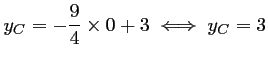 ,
et ainsi,
,
et ainsi,
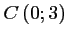 .
.
Les coordonnées du milieu de![$ [BC]$](/Generateur-Devoirs/1S/Chap3/ex7_c_img20.png) sont:
sont:
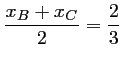 et
et
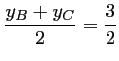 .
Il s'agit des coorodnnées de
.
Il s'agit des coorodnnées de 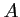 qui est donc bien le milieu de
qui est donc bien le milieu de
![$ [BC]$](/Generateur-Devoirs/1S/Chap3/ex7_c_img20.png) .
.
- Généralisation:
L'équation de la tangente en
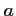 est:
est:
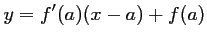 , soit
, soit
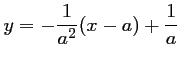 ,
et donc,
,
et donc,
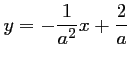 .
.
Cette tangente coupe l'axe des abscisses en
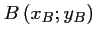 tel que
tel que 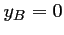 , et donc,
, et donc,
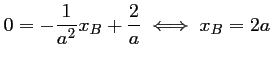 .
.
Elle coupe l'axe des ordonnées en
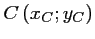 tel que
tel que
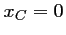 et donc,
et donc,
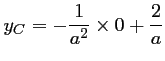 ,
d'où,
,
d'où,
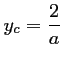 .
.
Les coordonnées du milieu de![$ [BC]$](/Generateur-Devoirs/1S/Chap3/ex7_c_img20.png) sont alors
sont alors
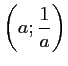 , c'est-à-dire les coordonnées du point
, c'est-à-dire les coordonnées du point 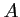 .
.
- Question bonus:
Pour tracer la tangente en un point
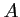 de
de
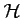 , on peut
par exemple:
, on peut
par exemple:
- construire
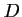 symétrique de
symétrique de 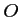 par rapport à
par rapport à 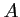
- construire
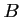 et
et 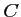 projections de
projections de 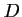 sur les axes
sur les axes
- comme
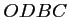 est un parallélogramme de centre
est un parallélogramme de centre 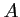 ,
,
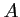 est le milieu de
est le milieu de ![$ [BC]$](/Generateur-Devoirs/1S/Chap3/ex7_c_img20.png) et donc, d'après ce qui précède,
la droite
et donc, d'après ce qui précède,
la droite 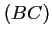 est la tangente à
est la tangente à
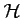 en
en 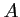 .
.
- construire
Cacher la correction
Tag:Fonctions et dérivées
Voir aussi:
