Malformation cardiaque et anévrisme
Exercice corrigé - Spécialité maths, première générale
Énoncé
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10%. L'étude a également permis de prouver que 30% des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8% pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements :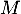
: « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
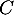: « La personne est victime d'un accident cardiaque au cours de sa vie ».
On choisit au hasard une personne dans la population française et on considère les évènements :
: « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
: « La personne est victime d'un accident cardiaque au cours de sa vie ».
-
- Quelle est la probabilité que la personne présente une malformation cardiaque de type anévrisme et soit victime d'un accident cardiaque au cours de sa vie.
- Calculer
.
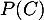- On choisit au hasard une victime d'un accident cardiaque. Quelle est la probabilité qu'elle présente une malformation cardiaque de type anévrisme ?
Correction
![\[\psset{xunit=1.5cm,yunit=1cm}
\begin{pspicture}(-2,-2.)(5,2)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$M$}\rput(0.7,1.2){$0,10$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$C$}\rput(2.7,2.2){$0,30$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{C}$}\rput(2.7,0.7){$0,70$}
%
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{M}$}\rput(0.7,-1.2){$0,90$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$C$}\rput(2.7,-0.7){$0,08$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{C}$}\rput(2.7,-2.2){$0,92$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exsecu_c/1.png)
Correction
On peut construire l'arbre pondéré suivant:-
-
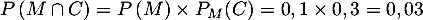
- En utilisant l'arbre (ou d'après la formule des probabilités totales):
![\[\begin{array}{ll}
P(C)&=P\left( M \cap C\right) + P\left(\overline M \cap C\right)\\[0.3cm]
&= P(M)\times P_M(C) + P\lp\overline M\rp\times P_{\overline M}(C) \\[0.3cm]
&= 0,1\times 0,3 + 0,9 \times 0,08 = 0,03 + 0,072 = 0,102\enar\]](/Generateur-Devoirs/1S/Chap7/exsecu_c/3.png)
-
- On choisit au hasard une victime d'un accident cardiaque.
La probabilité qu'elle présente une malformation cardiaque de type anévrisme est
:
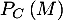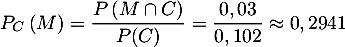
Tag:Probabilités conditionnelles
Autres sujets au hasard:
Voir aussi: