Loi d'une variable aléatoire
Exercice corrigé - Spécialité maths, première générale
Énoncé
On donne la loi de probabilité de d'une variable aléatoire 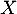 :
:
![\[\renewcommand{\arraystretch}{2.8}
\begin{tabular}{|*6{c|}}\hline
$x_i$ & $-2$ & $1$ & $2$ & $3$ & $5$ \\\hline
$P\left( X=x_i\rp$ & $\dfrac14$ & $\dfrac13$ & $\dfrac14$ & $\dfrac1{12}$ & $\dfrac1{12}$\\
\hline\end{tabular}\]](/Generateur-Devoirs/1S/ChapVA/ex1/2.png)
![\[\renewcommand{\arraystretch}{2.8}
\begin{tabular}{|*6{c|}}\hline
$x_i$ & $-2$ & $1$ & $2$ & $3$ & $5$ \\\hline
$P\left( X=x_i\rp$ & $\dfrac14$ & $\dfrac13$ & $\dfrac14$ & $\dfrac1{12}$ & $\dfrac1{12}$\\
\hline\end{tabular}\]](/Generateur-Devoirs/1S/ChapVA/ex1/2.png)
- Déterminer la probabilité
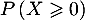 .
.
- Calculer l'espérance de
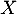 .
.
- Calculer l'écart type de
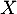 .
.
Correction
Correction
- On a
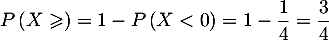
- L'espérance est
![\[E(X)=
\dfrac14\tm(-2)+\dfrac13\tm1+\dfrac14\tm2+\dfrac1{12}\tm3+\dfrac1{12}\tm5
=\dfrac{12}{12}=1
\]](/Generateur-Devoirs/1S/ChapVA/ex1_c/2.png)
- La variance est
![\[\begin{array}{ll}V(X)&=
\dfrac14\tm(-2-1)^2+\dfrac13\tm(1-1)^2+\dfrac14\tm(2-1)^2+\dfrac1{12}\tm(3-1)^2+\dfrac1{12}\tm(5-1)^2\\[.8em]
&=\dfrac{9}{4}+0+\dfrac{1}{4}+\dfrac{4}{12}+\dfrac{16}{12}\\[.8em]
&=\dfrac{50}{12}=\dfrac{25}{6}
\enar\]](/Generateur-Devoirs/1S/ChapVA/ex1_c/3.png)
L'écart type est alors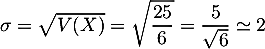
Tag:Variables aléatoires
Voir aussi:
