Calcul de distance dans un rectangle avec coordonnées
Exercice corrigé - Spécialité maths, première générale
Énoncé
Calcul d'une distance
![]() est un rectangle de dimensions
est un rectangle de dimensions ![]() et
et ![]() (
(![]() ).
).
![]() et
et ![]() sont les projetés orthogonaux des points
sont les projetés orthogonaux des points ![]() et
et ![]() sur
la droite
sur
la droite ![]() .
.
Le plan est muni d'un repère orthonormal
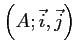 ,
dans lequel les points
,
dans lequel les points ![]() et
et ![]() ont pour coordonnées
ont pour coordonnées
![]() et
et ![]() .
.
|
![\begin{pspicture}(-0.5,0.2)(4,3.4)
\psline[linewidth=1.5pt]{->}(0,0)(1.66,0)\rp...
...t(-0.2,3.2){$D$}
\rput(1.5,2.45){$A'$}
\rput(3.5,0.5){$C'$}
%
\end{pspicture}](/Generateur-Devoirs/1S/Chap6/ex8_img18.png)
|
Correction
Correction
- Les projetés orthogonaux de
 et
et 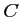 sur la droite
sur la droite 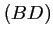 sont
respectivement
sont
respectivement 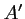 et
et 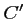 , et donc,
, et donc,
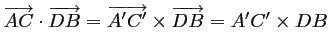 , car
, car
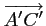 et
et
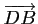 sont colinéaires et de même sens.
sont colinéaires et de même sens.
- On a les coordonnées:
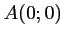 et
et 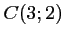 d'où
d'où
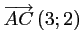 ,
et
,
et
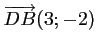 .
.
Ainsi,
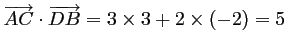 .
.
- D'après les questions précédentes, on a donc:
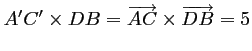 ,
d'où
,
d'où
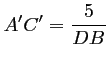 .
.
Or, d'après le théorème de Pythagore,
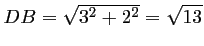 ,
d'où,
,
d'où,
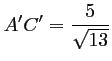 .
.
Tag:Produit scalaire
Voir aussi:
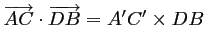 .
.
