Suite géométrique complexe
Exercice corrigé - Maths expertes, terminale générale
Énoncé
On considère la suite 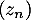 définie par
définie par 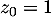 et, pour tout entier naturel
et, pour tout entier naturel 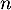 ,
, 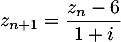 .
.
- Exprimer
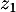 sous forme algébrique.
sous forme algébrique.
- Pour tout entier naturel
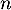 , on pose
, on pose 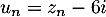 .
.
Exprimer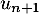 en fonction de
en fonction de 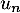 .
Quelle est la nature de la suite
.
Quelle est la nature de la suite 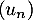 ?
?
- En déduire une expression de
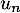 puis de
puis de 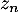 en fonction de
en fonction de 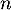 .
.
Correction
Correction
-
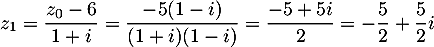
-
![\[\begin{array}{ll}u_{n+1}&=z_{n+1}-6i\\[.4em]
&=\dfrac{z_n-6}{1+i}-6i\\[1em]
&=\dfrac{z_n-6-6i(1+i)}{1+i}\\[1em]
&=\dfrac{z_n-6i}{1+i}\\[1em]
&=\dfrac{u_n}{1+i}\\[1em]
&=\dfrac1{1+i}u_n
\enar\]](/Generateur-Devoirs/Mex/CplxAlg/exsuite_c/2.png)
ce qui montre que la suite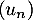 est géométrique de raison
est géométrique de raison 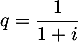
- On déduit des calculs précédents que, pour tout entier
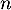 , on a
, on a
![\[\begin{array}{ll}u_n=u_0q^n&=(z_0-6i)\lp\dfrac1{1+i}\rp^n\\
&=\dfrac{1-6i}{(1+i)^n}\enar\]](/Generateur-Devoirs/Mex/CplxAlg/exsuite_c/6.png)
et donc, en revenant à la suite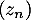 ,
,
![\[\begin{array}{lrl}&u_n&=z_-6i\\
\iff&z_n&=u_n+6i\\[.4em]
&&=\dfrac{1-6i}{(1+i)^n}+6i\enar\]](/Generateur-Devoirs/Mex/CplxAlg/exsuite_c/8.png)
Tag:Nombres Complexes - Algébrique
Voir aussi:
Quelques devoirs
sur les nombres complexes: forme algébrique des nombres complexes et résolution d'équations complexes
sur les nombres complexes: résolution d'équations et forme algébrique. Arithmétique, divisibilité et division euclidienne
sur les nombres complexes, point de vue algébrique. Calculs algébriques sur les nombres complexes, inverse d'un nombre complexe et résolution d'équations
sur les nombres complexes et polynômes. Résolution d'une éuqation complexe. Racine d'un polynôme et factorisation du polynôme. Quotients et restes de division euclidienne. Divisiblité par 8
