Une suite récurrente, sa conjecture, son python, et démonstration par récurrence
Exercice corrigé - Spécialité maths, terminale générale
On considère la suite 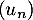 définie par:
définie par:
 et, pour tout entier naturel
et, pour tout entier naturel 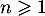 ,
,
![\[u_{n+1}=\lp1+\dfrac2n\right) u_n+\dfrac{18}{n}-4\,.\]](/Generateur-Devoirs/TS/ChapSuites/ex01.2/4.png)
- Calculer
 et
et 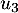 .
Quelle conjecture peut-on faire quant à la nature de la suite
.
Quelle conjecture peut-on faire quant à la nature de la suite
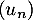 .
.
- Qu'affiche l'exécution du programme Python suivant ?
![\[\fbox{\begin{minipage}{5.4cm}
u=-5\\[.4em]
for n in range(1,5):\\[.4em]
\hspace*{1cm}u=(1+2/n)*u+18/n-4\\[.4em]
\hspace*{1cm}print(u)
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapSuites/ex01.2/8.png)
- Démontrer que, pour tout entier naturel
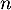 non nul,
non nul,
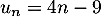 .
.
Correction
Cacher la correction
-
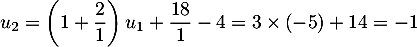 ;
;
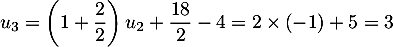
On peut conjecturer que la suite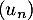 est arithmétique de
raison
est arithmétique de
raison  .
.
- Ce programme calcule et affiche les premières valeurs
de la suite:
 ,
, 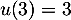 ,
, 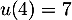 et
et  .
.
-
Initialisation: On a
 , et
pour
, et
pour  ,
,  .
.
Ainsi, initialement au rang , on a bien
, on a bien 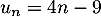 .
.
Hérédité: Supposons que pour un certain entier , on ait
, on ait
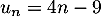 , alors,
, alors,
![\[\begin{array}{ll}
u_{n+1}&=\lp1+\dfrac2n\right) u_n+\dfrac{18}{n}-4\\[1.2em]
&=\lp1+\dfrac2n\right) \lp 4n-9\right)+\dfrac{18}{n}-4\\[1.2em]
&=4n-9+\dfrac{8n}{n}-\dfrac{18}{n}+\dfrac{18}{n}-4\\[.5em]
&=4n-5\\[.5em]
&=4(n+1)-9
\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex01.2_c/16.png)
Ainsi au rang on a bien encore
on a bien encore 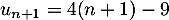 .
.
Conclusion: On a donc démontré, d'après le principe de récurrence, que pour tout entier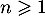 ,
,
 .
.
Cacher la correction
Tag:Suites
Voir aussi:
