Sujet 0, Bac 2021: Équation différentielle, exponentielle, suite
Exercice corrigé - Spécialité maths, terminale générale
Dans une boulangerie, les baguettes sortent du four à une température de 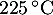 .
.
On s’intéresse à l’évolution de la température d’une baguette après sa sortie du four.
On admet qu’on peut modéliser cette évolution à l’aide d’une fonction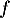 définie et dérivable sur l’intervalle
définie et dérivable sur l’intervalle 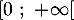 .
.
Dans cette modélisation,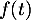 représente la température en degré Celsius de la baguette au bout de la durée
représente la température en degré Celsius de la baguette au bout de la durée 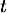 , exprimée en heure, après la sortie du four.
, exprimée en heure, après la sortie du four.
Ainsi,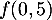 représente la température d’une baguette une demi-heure après la sortie du four.
représente la température d’une baguette une demi-heure après la sortie du four.
Dans tout l’exercice, la température ambiante de la boulangerie est maintenue à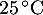 .
.
On admet alors que la fonction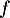 est solution de l'équation différentielle
est solution de l'équation différentielle 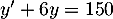 .
.
Correction
On s’intéresse à l’évolution de la température d’une baguette après sa sortie du four.
On admet qu’on peut modéliser cette évolution à l’aide d’une fonction
Dans cette modélisation,
Ainsi,
Dans tout l’exercice, la température ambiante de la boulangerie est maintenue à
On admet alors que la fonction
-
- Préciser la valeur de
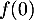 .
.
- Résoudre l'équation différentielle
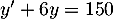 .
.
- En déduire que pour tout réel
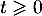 , on a
, on a 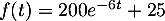 .
.
- Préciser la valeur de
- Par expérience, on observe que la température d’une baguette sortant du four :
- décroît ;
- tend à se stabiliser à la température ambiante.
La fonction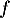 fournit-elle un modèle en accord avec ces observations ?
fournit-elle un modèle en accord avec ces observations ?
- Montrer que l’équation
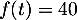 admet une unique solution dans
admet une unique solution dans 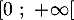 .
.
Pour mettre les baguettes en rayon, le boulanger attend que leur température soit inférieure ou égale à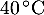 . On note
. On note 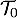 le temps d’attente minimal entre la sortie du four d’une baguette et sa mise en rayon.
le temps d’attente minimal entre la sortie du four d’une baguette et sa mise en rayon.
On donne en page suivante la représentation graphique de la fonction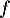 dans un repère orthogonal.
dans un repère orthogonal.
(\n,260)}
\multido{\n=0+20}{14}{\psline[linewidth=0.3pt,linecolor=lightgray](0,\n)(2.1,\n)}
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=20]{->}(0,0)(0,0)(2.1,260)
\psplot[linewidth=1.25pt,linecolor=blue,plotpoints=5000]{0}{2.1}{2.71828 x 6 mul neg exp 200 mul 25 add}
\uput[d](1.75,-15){\footnotesize Dur\'ee en heure}
\uput[r](0,250){\footnotesize Temp\'erature en degr\'e Celsius}
\uput[ur](0.3,60){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapEqDiff/ex0/20.png)
- Avec la précision permise par le graphique, lire
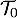 . On donnera une valeur approchée de
. On donnera une valeur approchée de 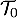 sous forme d’un nombre entier de minutes.
sous forme d’un nombre entier de minutes.
- On s’intéresse ici à la diminution, minute après minute, de la température d’une baguette à sa sortie du four.
Ainsi, pour un entier naturel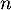 ,
, 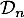 désigne la diminution de température en degré Celsius d’une baguette entre la
désigne la diminution de température en degré Celsius d’une baguette entre la 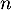 -ième et la
-ième et la 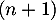 -ième minute après sa sortie du four.
-ième minute après sa sortie du four.
On admet que, pour tout entier naturel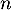 :
:
![\[\mathcal{D}_n=f\left(\dfrac{n}{60}\right)-f\left(\dfrac{n+1}{60}\right).\]](/Generateur-Devoirs/TS/ChapEqDiff/ex0/28.png)
- Vérifier que 19 est une valeur approchée de
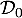 à 0,1 près, et interpréter ce résultat dans le contexte de l’exercice.
à 0,1 près, et interpréter ce résultat dans le contexte de l’exercice.
- Vérifier que l’on a, pour tout entier naturel
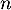 :
:
![\[\mathcal{D}_n = 200 e^{-0,1n}\left(1 - e^{-0,1}\right).\]](/Generateur-Devoirs/TS/ChapEqDiff/ex0/31.png)
En déduire le sens de variation de la suite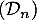 , puis la limite de la suite
, puis la limite de la suite 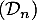 .
.
Ce résultat était-il prévisible dans le contexte de l’exercice ?
- Vérifier que 19 est une valeur approchée de
Correction
Tags:Équations différentiellesSuitesExponentielle
Voir aussi:
