Suite récurrente et suite intermédiaire géométrique avec logarithme
Exercice corrigé - Spécialité maths, terminale générale
On considère la suite 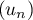 définie par
définie par
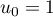 et, pour tout entier
et, pour tout entier 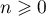 ,
,
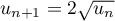 .
.
- Calculer
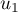 ,
, 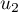 ,
, 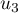 et
et 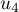 .
Donner les résultats sous la forme
.
Donner les résultats sous la forme 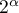 .
.
- On considère la suite
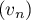 définie par
définie par
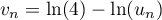 .
.
Montrer que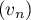 est une suite géométrique de raison
est une suite géométrique de raison  .
.
- Exprimer
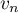 en fonction de
en fonction de 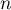 .
.
- Déterminer la limite de
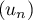 .
.
Correction
Cacher la correction
-
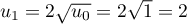

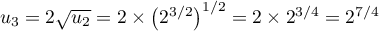
- Pour tout entier
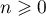 , on a
, on a
![\[\begin{array}{ll}
v_{n+1}&=\ln(4)-\ln\left( u_{n+1}\rp\\[.8em]
&=\ln(4)-\ln\lp2\sqrt{u_n}\rp\\[.8em]
&=\ln(4)-\lp\ln(2)+\ln(\sqrt{u_n})\rp\\[.8em]
&=\ln(4)-\ln(2)-\dfrac12\ln(u_n)\\[.8em]
&=\ln(4)-\dfrac12\ln(4)-\dfrac12\ln(u_n)\\[.8em]
&=\dfrac12\lp\ln(u_n)-\ln(4)\right)
=\dfrac12v_n
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2_c/5.png)
ce qui montre que la suite est géométrique de raison
est géométrique de raison  .
.
- Comme
 ,
on en déduit que
,
on en déduit que
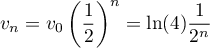 .
.
Ensuite, comme
![\[v_n=\ln(u_n)-\ln(4)=\ln\lp\dfrac{u_n}4\right)
\iff \dfrac{u_n}4=e^{v_n}
\iff u_n=4e^{v_n}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2_c/10.png)
- Comme
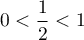 , on a
, on a  et alors,
comme
et alors,
comme 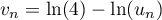 , on en déduit que
, on en déduit que
![\[\dsp\lim_{n\to+\infty}\ln(4)-\ln(u_n)=0
\iff \lim_{n\to+\infty}\ln(u_n)=\ln(4)
\iff \lim_{n\to+\infty}u_n=4\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2_c/14.png)
Cacher la correction
Tags:LogarithmeSuites
Voir aussi:
