Bac 2023 - Logarithme, variation, limites et TVI

Exercice corrigé - Spécialité maths, terminale générale

On considère la fonction $f$ définie sur $]0~;~+\infty[$ par
\[f(x) = x^2 - 8\ln (x)\]

où ln désigne la fonction logarithme népérien.
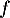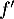On admet que $f$ est dérivable sur $]0~;~+\infty[$, on note $f'$ sa fonction dérivée.


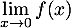  1. Déterminer $\displaystyle\lim_{x \to 0} f(x)$.
  2. On admet que, pour tout $x > 0$,  $f(x) = x^2\left(1 - 8\dfrac{\ln (x)}{x^2}\right)$.
    En déduire la limite: $\displaystyle\lim_{x \to + \infty} f(x)$.
  3. Montrer que, pour tout réel 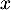$x$ de $]0~;~+\infty[$, $f'(x) = \dfrac{2\left(x^2 - 4\right)}{x}$.
  4. Étudier les variations de $f$ sur $]0~;~+\infty[$ et dresser son tableau de variations complet.
    On précisera la valeur exacte du minimum de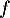 $f$ sur $]0~;~+\infty[$.
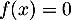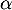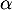  5. Démontrer que, sur l'intervalle ]0 ; 2], l'équation $f(x) = 0$ admet une solution unique $\alpha$ (on ne cherchera pas à déterminer la valeur de $\alpha$).
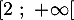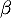  6. On admet que, sur l'intervalle $[2~;~ +\infty[$, l'équation $f(x) = 0$ admet une solution unique $\beta$ (on ne cherchera pas à déterminer la valeur de $\beta$).
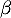    En déduire le signe de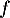 $f$ sur l'intervalle $]0~;~+\infty[$.
  7. Pour tout nombre réel 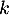$k$, on considère la fonction 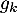$g_k$ définie sur $]0~;~+\infty[$ par:
    \[g_k(x) = x^2 - 8\ln (x) + k.\]


    En s'aidant du tableau de variations de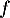 $f$, déterminer la plus petite valeur de 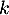$k$ pour laquelle la fonction $g_k$ est positive sur l'intervalle $]0~;~+\infty[$.

Correction


Tag:Logarithme

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs


LongPage: h2: 1 - h3: 0