Probabilité de l'intersection
Exercice corrigé - Spécialité maths, terminale générale
Une entreprise fabrique des cartes à puces. Chaque puce peut présenter deux défauts notés A et B.
Une étude statistique montre que 2,8% des puces ont le défaut A,
2,2% des puces ont le défaut B et, heureusement, 95,4% des puces
n'ont aucun des deux défauts.
Quelle est la probabilité qu'une puce prélevée au hasard ait les deux défauts ?
Quelle est la probabilité qu'une puce prélevée au hasard ait les deux défauts ?
Correction
D'après QCM, Bac centres étrangers, 9 juin 2021
On note A et B les événements: "la puce a le défaut A" et "la puce a le défaut B", et l'énoncé se traduit alors par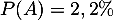
, 
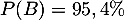et
,
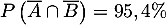ou encore le diagramme de Venn
(4,2)(4,-2)(-4,-2)
\rput[l](-3.8,1.6){95,4\%}
\psellipse[fillstyle=solid,,fillcolor=white](-1,0)(1.8,1)
\rput[l](-2.4,.3){A}
\rput[l](-2.4,-.1){2,8\%}
\psellipse[fillstyle=solid,fillcolor=white](1,0)(1.8,1)
\rput[r](2.4,.3){B}
\rput[r](2.4,-.1){2,2\%}
\begin{psclip}{%
\psellipse(-1,0)(1.8,1)}
\psellipse[fillstyle=vlines](1,0)(1.8,1)
\end{psclip}
\psellipse[linestyle=none,fillstyle=solid,fillcolor=white](0.05,0)(.25,.3)
\rput(0,0){\large\bf\red ?}
\end{pspicture}
\]](/Generateur-Devoirs/TS/ChapProbabilites/inter_c/4.png)
En utilisant le diagramme de Venn précédent, on a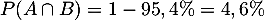
puis
![\[P(A\cap B)=P(A)+P(B)-P(A\cup B)
=2,8\%+2,2\%-4,6\%=0,4\%\]](/Generateur-Devoirs/TS/ChapProbabilites/inter_c/6.png)
Cacher la correction
D'après QCM, Bac centres étrangers, 9 juin 2021
On note A et B les événements: "la puce a le défaut A" et "la puce a le défaut B", et l'énoncé se traduit alors par
,
et
,
ou encore le diagramme de Venn
En utilisant le diagramme de Venn précédent, on a
puis
Cacher la correction
Tag:Probabilités
Autres sujets au hasard:
Voir aussi: