Bac 2022 (12 mai): Arbre et loi binomiale
Exercice corrigé - Spécialité maths, terminale générale
Le coyote est un animal sauvage proche du loup, qui vit en Amérique du Nord.
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
On note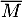
et 
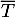respectivement les évènements contraires de M et T.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de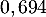
.
Correction
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
- Si le coyote est malade, le test est positif dans 97 % des cas.
- Si le coyote n'est pas malade, le test est négatif dans 95 % des cas.
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
- M: « le coyote est malade »;
- T: « le test du coyote est positif ».
On note
et respectivement les évènements contraires de M et T.
- Recopier et compléter l'arbre pondéré ci-dessous qui modélise la situation.
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$M$}
\rput(.8,.9){\dots}
\rput(.8,-1){\dots}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{M}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$T$}
\rput(2.8,1.7){\dots}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{T}$}
\rput(2.8,.2){\dots}
\rput(2.8,-.4){\dots}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{T}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$T$}
\rput(2.8,-1.8){\dots}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022/7.png)
- Déterminer la probabilité que le coyote soit malade et que son test soit positif.
- Démontrer que la probabilité de T est égale à
.
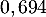- On appelle « valeur prédictive positive du test » la probabilité que le coyote soit effectivement malade sachant que son test est positif.
Calculer la valeur prédictive positive du test. On arrondira le résultat au millième. -
- Par analogie avec la question précédente, proposer une définition de la « valeur prédictive négative du test » et calculer cette valeur en arrondissant au millième.
- Comparer les valeurs prédictives positive et négative du test, et interpréter.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de
.
- Lorsqu'on capture au hasard cinq coyotes, on assimile ce choix à un tirage avec remise.
On note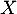
la variable aléatoire qui à un échantillon de cinq coyotes capturés au hasard associe le nombre de coyotes dans cet échantillon ayant un test positif.
- Quelle est la loi de probabilité suivie par
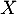? Justifier et préciser ses paramètres.
- Calculer la probabilité que dans un échantillon de cinq coyotes capturés au hasard, un seul ait un test positif. On arrondira le résultat au centième.
- Un vétérinaire affirme qu'il y a plus d'une chance sur deux qu'au moins quatre coyotes sur cinq aient un test positif : cette affirmation est-elle vraie ? Justifier la réponse.
- Quelle est la loi de probabilité suivie par
- Pour tester des médicaments, les vétérinaires ont besoin de disposer d'un coyote présentant un test positif. Combien doivent-ils capturer de coyotes pour que la probabilité qu'au moins l'un d'entre eux présente un test positif soit supérieure à
?
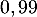Correction
Tag:Probabilités
Autres sujets au hasard:
Voir aussi: