Oral de Bac - suite récurrente - Conjectures graphiques et récurrence
Exercice corrigé - Spécialité maths, terminale générale
On considère la suite 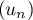 définie par
définie par 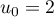 et,
pour tout entier
et,
pour tout entier 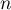 ,
, 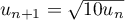 .
.
On note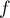 la fonction définie par l'expression
la fonction définie par l'expression
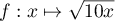 .
.
Correction
On note
- Tracer l'allure de la courbe représentative de la fonction
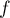 et construire sur l'axe des abscisses les premiers termes
et construire sur l'axe des abscisses les premiers termes 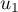 ,
,
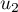 , … de la suite
, … de la suite 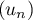 .
.
Quelles conjectures peut-on faire ?
- Démontrer que la suite
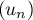 est croissante, positive et
majorée par 10.
est croissante, positive et
majorée par 10.
- En déduire que
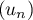 converge vers une limite
converge vers une limite 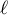 .
.
Déterminer cette limite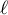 .
.
Correction
Tag:Suites
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
