Oral de Bac - suite récurrente affine - Conjectures graphiques et suite auxiliaire géométrique
Exercice corrigé - Spécialité maths, terminale générale
Soit 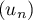 la suite définie par
la suite définie par 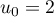 et
et
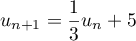 .
.
- Calculer
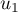 et
et  .
.
- Tracer les droites d'équations
 et
et 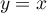 .
Construire sur ce graphique les premières termes
.
Construire sur ce graphique les premières termes  ,
, 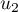 ,
, 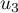 ,…
de la suite.
,…
de la suite.
Quelles conjectures peut-on faire ? - Soit
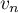 la suite définie par
la suite définie par 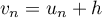 .
Déterminer le réel
.
Déterminer le réel 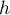 pour que la suite
pour que la suite 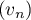 soit géométrique de
raison
soit géométrique de
raison 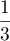 .
.
- Exprimer alors
 , puis
, puis 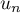 , en fonction de
, en fonction de 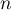 .
En déduire la limite de
.
En déduire la limite de 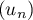 .
.
Correction
Cacher la correction
-
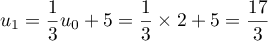 ;
;

-
![\psset{unit=0.8cm,arrowsize=7pt}
\begin{pspicture}(-1,-1)(10,10)
\psline{->}(-.5,0)(10,0)
\psline{->}(0,-.5)(0,10)
\newcommand{\f}[1]{1 3 div #1 mul 5 add}
\psplot[linewidth=1.4pt]{0}{9.5}{\f{x}}
\rput(10,7.3){$y=\dfrac13x+5$}
\psplot{-0.2}{9.5}{x}\rput(8.8,9.5){$y=x$}
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
\def\xinit{2}\def\nmax{4}
\psline[linestyle=dashed](\xinit,0)(!\xinit\space\f{\xinit})(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,-0.3){$u_0=2$}
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed](!\fn{\i}{\xinit} \space 0)(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.3){$u_\i$}
}
\def\ninf{20}
\psline[linecolor=blue](!\fn{\ninf}{\xinit}\space 0)(!\fn{\numexpr\ninf+1}{\xinit}\space\fn{\numexpr\ninf+1}{\xinit})(!0\space\fn{\numexpr\ninf+1}{\xinit})
\rput(!\fn{\ninf}{\xinit}\space -0.3){\blue$\ell$}
\rput(!-.3\space\fn{\ninf}{\xinit}){\blue$\ell$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/exOral03_c/3.png)
On peut conjecturer à partir de ce graphique que la suite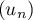 est croissante et converge vers l'abscisse
est croissante et converge vers l'abscisse 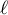 du point
d'intersection des deux droites, soit
du point
d'intersection des deux droites, soit 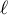 tel que
tel que
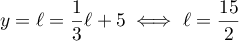 .
.
-
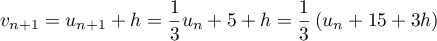 .
.
Pour que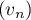 soit géométrique, on doit avoir
soit géométrique, on doit avoir
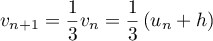 , et on doit ainsi avoir
, et on doit ainsi avoir
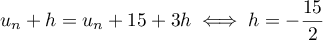 .
.
- On a
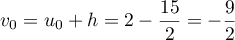 , et
alors
, et
alors  .
.
Comme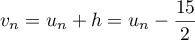 , on a donc
, on a donc 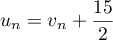 .
.
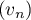 est une suite géométrique de raison
est une suite géométrique de raison  , et
donc,
, et
donc, 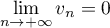 .
.
Ainsi,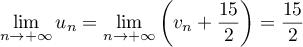 , et on démontre ainsi la limite
conjecturée à la question 2.
, et on démontre ainsi la limite
conjecturée à la question 2.
Cacher la correction
Tag:Suites
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
