Bac 2014 (Nouvelle Calédonie) - Suite récurrente, construction graphique, récurrence, somme des 1er termes et algorithme
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 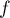 définie sur l'intervalle
définie sur l'intervalle 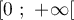 par
par
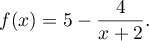
On admettra que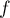 est dérivable sur l'intervalle
est dérivable sur l'intervalle 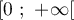 .
.
On a tracé en annexe 1 dans un repère orthonormé la courbe représentative de
représentative de 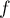 ainsi que la droite
ainsi que la droite 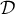 d'équation
d'équation 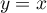 .
.
Annexe 1 à rendre avec la copie
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=4000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC/45.png)
Annexe 2 à rendre avec la copie

Correction
On admettra que
On a tracé en annexe 1 dans un repère orthonormé la courbe
- Démontrer que
 est croissante sur l'intervalle
est croissante sur l'intervalle 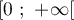 .
.
- Résoudre l'équation
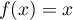 sur l'intervalle
sur l'intervalle 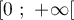 . On note
. On note 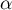 la solution.
la solution.
On donnera la valeur exacte de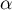 puis on en donnera une valeur approchée à
puis on en donnera une valeur approchée à 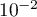 près.
près.
- On considère la suite
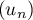 définie par
définie par 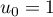 et, pour tout entier naturel
et, pour tout entier naturel 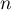 ,
, 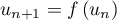 .
.
Sur la figure de annexe 1, en utilisant la courbe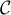 et la droite
et la droite 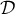 , placer les points
, placer les points 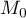 ,
, 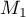 et
et 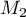 d'ordonnée nulle et d'abscisses respectives
d'ordonnée nulle et d'abscisses respectives 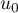 ,
, 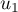 et
et 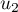 .
.
Quelles conjectures peut-on faire sur le sens de variation et la convergence de la suite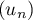 ?
?
-
- Démontrer, par récurrence, que, pour tout entier naturel
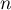 ,
,
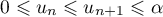
où est le réel défini dans la question 2.
est le réel défini dans la question 2.
- Peut-on affirmer que la suite
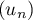 est convergente ? On justifiera la réponse.
est convergente ? On justifiera la réponse.
- Démontrer, par récurrence, que, pour tout entier naturel
- Pour tout entier naturel
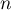 , on définit la suite
, on définit la suite 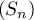 par
par
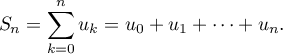
- Calculer
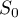 ,
, 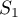 et
et 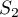 . Donner une valeur approchée des résultats à
. Donner une valeur approchée des résultats à 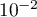 près.
près.
- Compléter l'algorithme donné en annexe 2 pour qu'il affiche la somme
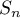 pour la valeur de l'entier
pour la valeur de l'entier 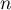 demandée à l'utilisateur.
demandée à l'utilisateur.
- Montrer que la suite
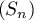 diverge vers
diverge vers 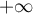 .
.
- Calculer
Annexe 1 à rendre avec la copie
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=4000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC/45.png)
Annexe 2 à rendre avec la copie

Correction
Tag:Suites
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
