logarithme, asymptote oblique et position relative et calcul d'aire
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 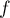 définie sur l'intervalle
définie sur l'intervalle 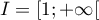 par:
par: 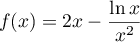 .
.
On note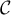 sa courbe représentative.
sa courbe représentative.
On note
- Montrer que la droite
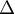 d'équation
d'équation 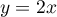 est une asymptote à
est une asymptote à 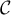 en
en 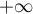 .
.
- Etudier la position relative de la courbe
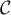 et de la
droite
et de la
droite 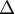 .
.
- On admet que
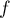 est strictement croissante sur
est strictement croissante sur 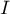 .
Tracer dans un repère l'allure de
.
Tracer dans un repère l'allure de 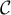 .
.
On prendra comme unités: 2cm sur l'axe des abscisses et 1cm sur l'axe des ordonnées. - Soit
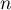 un entier naturel non nul.
un entier naturel non nul.
On considère le domaine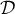 du plan compris entre la
courbe
du plan compris entre la
courbe 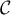 , la droite
, la droite 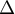 , et les
droites d'équations respectives
, et les
droites d'équations respectives 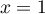 et
et 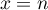 .
.
- Justifier que cette aire, exprimée en
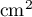 , est donnée
par:
, est donnée
par:
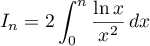 .
.
- Montrer que la fonction
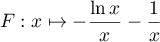 est une primitive de la fonction
est une primitive de la fonction 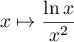 sur
sur
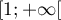 .
.
- En déduire une expression de
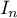 en fonction de
en fonction de 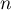 .
.
- Calculer la limite de l'aire du domaine
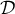 quand
quand 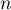 tend vers
tend vers 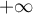 .
.
- Justifier que cette aire, exprimée en
Correction
(D'après Liban 2012)
On considère la fonction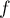 définie sur l'intervalle
définie sur l'intervalle 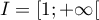 par:
par: 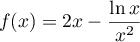 .
.
On note sa courbe représentative.
sa courbe représentative.
Cacher la correction
(D'après Liban 2012)
On considère la fonction
On note
- Pour tout
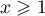 , on a
, on a
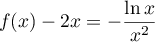 ,
et donc, par croissances comparées,
,
et donc, par croissances comparées,
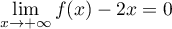 .
.
Ainsi, la droite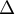 d'équation
d'équation 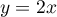 est une asymptote à
est une asymptote à 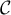 en
en 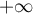 .
.
- Pour tout
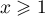 ,
, 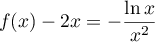 .
.
Or, pour tout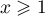 ,
, 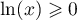 ,
et
,
et 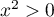 , et donc,
, et donc,
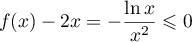 :
:
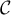 est toujours au dessous de
est toujours au dessous de 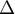 sur
sur 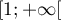 .
.
-
(1,2)(0,2)
\rput(1.1,1.3){1}\rput(.6,2){2}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex7_c/21.png)
-
- L'aire de
 est, compte tenu de l'unité d'aire de 2
est, compte tenu de l'unité d'aire de 2
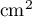 de notre graphique, et de la linéarité de l'intégrale,
de notre graphique, et de la linéarité de l'intégrale,
![\[I_n=2\left( \int_1^n f(x)\,dx-\int_1^n 2x\,dx\right)
=2\int_1^n \left( f(x)-2x\right) dx
=2\int_0^n \dfrac{\ln x}{x^2}\,dx
\]](/Generateur-Devoirs/TS/ChapIntegration/ex7_c/24.png)
- Pour tout
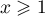 ,
,
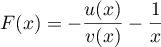 ,
avec
,
avec 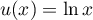 , donc
, donc 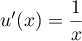 et
et 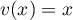 , donc
, donc 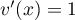 .
.
Ainsi,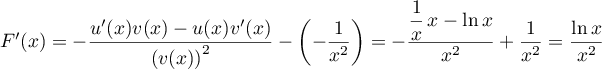
Ainsi, est bien une primitive de la fonction
est bien une primitive de la fonction 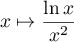 sur
sur  .
.
- On en déduit que
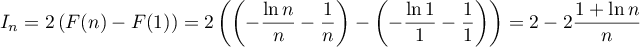
- Comme
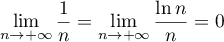 , par
croissances comparées, la limite de l'aire du domaine
, par
croissances comparées, la limite de l'aire du domaine 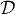 quand
quand 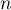 tend vers
tend vers 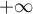 est:
est: 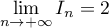 .
.
- L'aire de
Cacher la correction
Tags:IntégralesFonctionsPrimitive
Voir aussi:
