Fonctions et intégrales
Exercice corrigé - Spécialité maths, terminale générale
On donne le tableau de variation d'une fonction 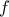 dérivable sur
dérivable sur
 :
:
 dérivable sur
dérivable sur
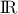 :
:
- On considère les intégrales suivantes:
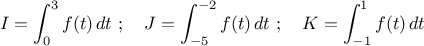
Pour une seule de ces intégrales on peut affirmer qu'elle est positive, et pour une seule on peut affirmer qu'elle est négative.
Préciser ces deux intégrales et justifier ce choix.
- A l'aide des informations contenues dans le tableau de variation
de
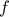 , donner un encadrement par des nombres entiers des intégrales
suivantes:
, donner un encadrement par des nombres entiers des intégrales
suivantes:
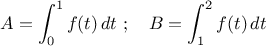
- On définit, pout tout réel
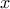 ,
la fonction
,
la fonction 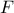 par
par 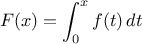 .
.
- Déterminer deux entiers naturels
 et
et 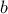 tels que
tels que
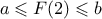 .
.
- Etudier la limite de
 lorsque
lorsque  tend vers
tend vers 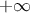 .
.
- Etudier le sens de variation de la fonction
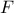 .
.
- Déterminer deux entiers naturels
Correction
Cacher la correction
- Comme la fonction
 est positive sur
est positive sur  ,
on a:
,
on a:
 .
.
Comme la fonction est négative sur l'intervalle
est négative sur l'intervalle  ,
on a:
,
on a:
 .
.
- Pour tout réel
 , on a:
, on a:  .
.
En intégrant pour allant de
allant de  à
à  , on obtient,
car l'intégrale conserve l'ordre,
, on obtient,
car l'intégrale conserve l'ordre,

De même, sur l'intervalle ,
,  , et
donc,
, et
donc,

-
- D'après la relation de Chasles:
 ,
d'où
,
d'où  .
.
- Pour tout réel
 ,
on a
,
on a  .
.
Ainsi, si ,
alors
,
alors
 .
.
Or, , et donc,
par comparaison (théorème des gendarmes),
on en déduit que
, et donc,
par comparaison (théorème des gendarmes),
on en déduit que  .
.
-
 est la primitive de
est la primitive de  qui s'nnule en
qui s'nnule en  , et ainsi,
, et ainsi,
 .
.
Comme est négative sur
est négative sur  ,
,
 est décroissante sur
est décroissante sur  ,
et comme
,
et comme  est positive sur
est positive sur  ,
,
 est croissante sur
est croissante sur  .
.
- D'après la relation de Chasles:
Cacher la correction
Tag:Intégrales
Voir aussi:
Quelques devoirs
intégration, Calculs d'intégrales - Suite d'intégrales (Bac S, 19 juin 2014) - Dimensionnement d'un récupérateur d'eau (Bac S - Amérique du nord, 1er juin 2016)
intégration, Calculs d'intégrales - Aire sous une courbe (Bac S - métropole, 11 septembre 2014) - Aire entre deux courbes (Bac S, juin 2008)
sur les intégrales: calcul d'intégrales, suite d'intégrales, et un calcul de volume
sur les intégrales: calcul d'intégrales, suite d'intégrales
