Fonction ln simple, TVI, convexité

Exercice corrigé - Spécialité maths, terminale générale

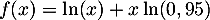On considère la fonction $f$ définie sur $]0;+\infty[$ par $f(x)=\ln(x)+x\ln(0,95)$.
  1. Étudier les variations de $f$.
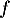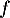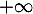  2. Déterminer les limites de $f$ en 0 et en $+\infty$.
  3. Montrer que $f(x)=0$ admet une unique solution $\beta$ sur $[20;+\infty[$.
    Donner un encadrement à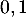 $0,1$ près de cette solution.
  4. Étudier la convexité de $f$.

Correction
(D'après Bac centres étrangers 10 juin 2021)
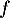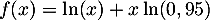On considère la fonction $f$ définie sur $]0;+\infty[$ par $f(x)=\ln(x)+x\ln(0,95)$.
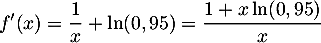
  1. On a $f'(x)=\dfrac1x+\ln(0,95)=\dfrac{1+x\ln(0,95)}{x}$
    \[\begin{tabular}{|c|ccccc|}\hline $x$ & $0$ && $-\dfrac1{\ln(0,95)}$ && $+\infty$ \\\hline $1+x\ln(0,95)$&& $+$ &0&$-$&\\\hline $x$&0&&$+$&&\\\hline $f'(x)$&& $+$ &0&$-$&\\\hline &&&&&\\ $f$&&\LARGE{$\nearrow$}&&\LARGE{$\searrow$}&\\ &&&&&\\\hline \end{tabular}\]


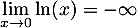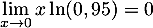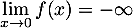  2. En 0, on a $\dsp\lim_{x\to0}\ln(x)=-\infty$ et $\dsp\lim_{x\to0}x\ln(0,95)=0$ et donc $\dsp\lim_{x\to0}f(x)=-\infty$.

    En $+\infty$, on a une forme indéterminée. On factorise donc:
    \[f(x)=x\lp\dfrac{\ln(x)}{x}+\ln(0,95)\rp\]

    où, par croissances comparées, $\dsp\lim_{x\to+\infty}\dfrac{\ln(x)}x=0$ et donc, comme $\ln(0,95)<0$, on obtient
    \[\lim_{x\to+\infty}f(x)=-\infty\]

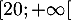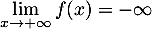  3. La fonction $f$ est continue et strictement décroissante sur $[20;+\infty[$, avec $f(20)\simeq2>0$ et $\dsp\lim_{x\to+\infty}f(x)=-\infty$ donc, d'après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), il existe une unique solution 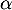$\alpha$ à l'équation $f(x)=0$.

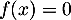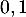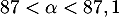
    Avec la calculatrice, on trouve l'encadrement, à $0,1$ près, $87<\alpha<87,1$
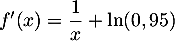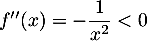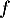  4. On a $f'(x)=\dfrac1x+\ln(0,95)$ et donc $f''(x)=-\dfrac1{x^2}<0$, d'où $f$ est concave sur $]0;+\infty[$.


Cacher la correction


Tags:LogarithmeConvexité

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs


LongPage: h2: 1 - h3: 0