Bac 2011 (Amérique du nord) - Étude de fonctions avec exponentielle, position relative, suite récurrente
Exercice corrigé - Spécialité maths, terminale générale
Partie A
On considère la fonction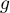 définie sur
définie sur 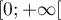 par
par
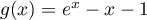 .
.
Partie B
On considère la fonction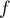 définie sur
définie sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/11.png) par
par
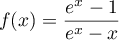 .
.
La courbe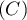 représentative de la fonction
représentative de la fonction 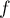 dans le plan muni
d'un repère orthonormal est donnée en annexe.
Cette annexe sera complétée et remise avec la copie à la fin de
l'épreuve.
dans le plan muni
d'un repère orthonormal est donnée en annexe.
Cette annexe sera complétée et remise avec la copie à la fin de
l'épreuve.
On admet que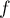 est strictement croissante sur
est strictement croissante sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/16.png) .
.
Partie C
On considère la suite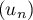 définie par:
définie par:
![$\la\begin{array}{ll} u_0=\dfrac12 \\[0.3cm] \text{pour tout entier naturel } n, u_{n+1}=f\left( u_n\rp\enar\right.](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/35.png) .
.
Annexe
Cette page sera complétée et remise avec la copie à la fin de l'épreuve.
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\psplot{0}{1}{2.718 x exp 1 sub 2.718 x exp x sub div}
\newcommand{\f}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\f{\i}\space-.2)(!\f{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\f{\i})(!1.5\space\f{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/39.png)
Correction
On considère la fonction
- Etudier les variations de la fonction
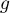 .
.
- Déterminer le signe de
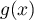 suivant les valeurs de
suivant les valeurs de 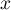 .
.
- En déduire que pour tout
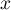 de
de  ,
, 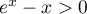 .
.
Partie B
On considère la fonction
La courbe
On admet que
- Montrer que pour tout
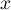 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/18.png) ,
, ![$f(x)\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/19.png) .
.
- Soit
 la droite d'équation
la droite d'équation 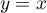 .
.
- Montrer que pour tout
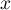 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/23.png) ,
, 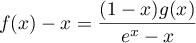 .
.
- Etudier la position relative de la droite
 et de la
courbe
et de la
courbe 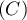 sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/27.png) .
.
- Montrer que pour tout
-
- Déterminer une primitive de
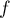 sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/29.png) .
.
- Calculer l'aire, en unité d'aire, du domaine du plan délimité
par la courbe
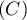 , la droite
, la droite  et les droites d'équations
et les droites d'équations
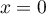 et
et  .
.
- Déterminer une primitive de
Partie C
On considère la suite
![$\la\begin{array}{ll} u_0=\dfrac12 \\[0.3cm] \text{pour tout entier naturel } n, u_{n+1}=f\left( u_n\rp\enar\right.](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/35.png) .
.
- Construire sur l'axe des abscisses les quatre premiers termes de la suite en laissant apparents les traits de construction.
- Montrer que pour tout entier
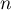 ,
,
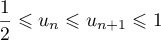 .
.
- En déduire que la suite
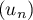 est convergente et
déterminer sa limite.
est convergente et
déterminer sa limite.
Annexe
Cette page sera complétée et remise avec la copie à la fin de l'épreuve.
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\psplot{0}{1}{2.718 x exp 1 sub 2.718 x exp x sub div}
\newcommand{\f}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\f{\i}\space-.2)(!\f{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\f{\i})(!1.5\space\f{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/39.png)
Correction
Tags:ExponentielleSuites
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
