Étude complète d'une fonction …
Exercice corrigé - Spécialité maths, terminale générale
Soit 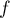 la fonction définie sur
la fonction définie sur 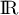 par
par 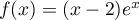 .
.
- Déterminer les limites de
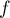 en
en  et
et 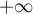 .
Interpréter graphiquement ces résultats.
.
Interpréter graphiquement ces résultats.
- Étudier les variations de
 .
.
- Tracer l'allure de la courbe de
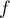 , en utilisant tous les résultats précédents.
, en utilisant tous les résultats précédents.
Correction
Soit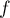 la fonction définie sur
la fonction définie sur 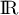 par
par 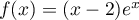 .
.
Cacher la correction
Soit
- En
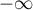 , on a
, on a 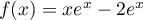 ,
où, par croissances comparées,
,
où, par croissances comparées,
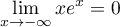 et comme
et comme
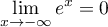 on a donc par addition des limites
on a donc par addition des limites
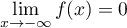 .
.
En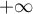 , on a
, on a 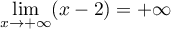 et
et 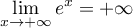 ,
d'où, par produit des limites,
,
d'où, par produit des limites,
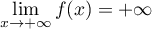 .
.
On en déduit que la droite d'équation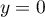 est une asymptote horizontale
à la courbe de
est une asymptote horizontale
à la courbe de 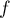 en
en 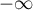 .
Il n'y a pas d'asymptote horizontale en
.
Il n'y a pas d'asymptote horizontale en 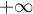 .
.
- On a
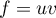 avec
avec 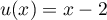 donc
donc 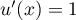 ,
et
,
et 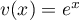 donc
donc 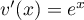 ,
et alors
,
et alors
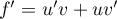 ,
soit
,
soit
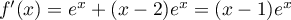 .
.
On peut alors dresser le tableau de variation de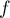 ,
,
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$-\infty$ && 1 && $+\infty$ \\\hline
$x-2$ && $-$ &0& $+$ &\\\hline
$e^x$ && $+$ &$|$& $+$ &\\\hline
$f'(x)$ && $-$ &0& $+$ &\\\hline
&0&&&&$+\infty$\\
$f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&$-e$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex0_c/25.png)
- On trace l'assymptote horizontale,
et on n'oublie pas non plus la tangente horizontale au point
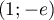 de la courbe.
de la courbe.
![\[\psset{xunit=2cm,yunit=1.5cm,arrowsize=8pt}
\begin{pspicture*}(-3.5,-3.)(3.5,2.7)
\psline{->}(-3.5,0)(3.5,0)
\psline{->}(0,-3)(0,2.7)
\psplot[linewidth=1.4pt]{-3.5}{3.5}{x 2 sub 2.718 x exp mul}
\psline[linecolor=blue](-4,0)(4,0)\rput(-1,.2){\blue$y=2$}
\rput(-.1,-.2){0}
\psline(-.1,-2.718)(.1,-2.718)\rput[r](-.15,-2.72){$-e$}
\psline[linestyle=dashed](0,-2.718)(1,-2.718)(1,0)
\rput(1,.2){1}
\psline[linecolor=red]{<->}(.4,-2.718)(1.6,-2.718)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex0_c/27.png)
Cacher la correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
